方案比较法的案例分析

某施工企业在5年前以50万元购回1台设备A。初估正常使用年限为10年,界时残值为15万元。在此期间,第1年的年使用费用为6万元,且每年按2%上升。年创产值17万元。目前市场上又出现了一种性能更优越的进口挖掘机,价格为80万元,平均年使用费用为5万元,按每年2%上升,年创产值为27万元。若正常使用年限为15年,界时残值为17万元。现如果卖出原设备,市场价为25万元。在这种情况下,原设备更新是否合理(企业定MARR=10%)?
为了便于换算,各项费用采用字母表示如下:
(1)现值,用P表示;(2)年金,用A表示;(3)终值,用F表示;(4)年利率,用i表示;(5)投资所获的逐年利率,用R表示;(6)企业最小诱人收益率,用MARR表示;(7)等额年使用费用,用C表示。
按企业定的MARR=10%为基准收益率,以上两种方案在以后使用中的等额年使用费用C1、C2,表示,年均成本投资用A1、A2表示,则:
 万元
万元
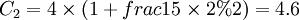 万元
万元
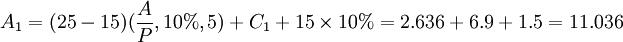 万元
万元
 万元
万元
两种方案的年均利润分别用R1、R2表示,则:
R1 = 17 − A1 = 17 − 11.036 = 5.964 万元
R2 = 27 − A2 = 27 − 11.5845 = 12.4155 万元
利用插值法比较两种方案的年利率,设两种方案的年利率分别为i1、i2,则:

——方案1的等额资金恢复系数。
fracR1P1 = frac5.9625 = 0.2386
式中:n=5。查复利系数表可知:
i=6%时,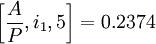
i=7%时,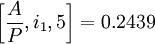
所以: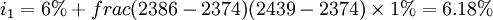
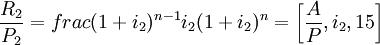
——方案2的等额资金恢复系数。
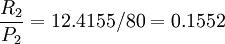
式中:n=15。i2为方案2的实际年利率,查复利系数表可知:
i=13%时,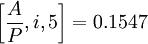
i=14%时,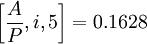
所以: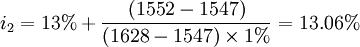
有:i2 > MARR > i1
由以上不等式可知,方案2的年利率大于企业最小诱人收益率,可采用。方案1的收益率小于企业最小诱人收益率,不可行。
若方案1在其它条件等同的情况下,要达到方案2的收益所需的现值投资设为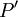 ,则:
,则:
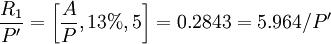
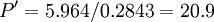 万元
万元
以上的经济含义是在方案1的其它条件等同情况下,若采用方案2,可使其现金投资节约25一20.9=4.1万元。
结论(1)旧设备帐面价值为17+(50一17)/2=33.5万元,目前市场价为25万元,沉没成本为33.5一25=8.5万元。这是一笔无法挽回的资金。其原因是5年前购买设备时决策所致。
(2)A设备的使用使收益率大大增加。不但超出旧设备的7个百分点,也超出了企业最小诱人收益率3个百分点。
(3)在更换设备后,虽然沉没成本达8.5万元,但由于新设备、新技术的应用,仍可得到4.1万元的现金节约。
(4)自更换设备之日起,由于新设备与旧设备相比,将来的使用年限将多出10年,因此从长远角度看,更新设备将更具有现实意义。
由以上的例子可看出,方案比较法在设备综合管理中起着举足轻重的作用。由此分析得出的结论,只要数据正确,方法对头,它就具有科学性,其结果自然是可信的,因此也就可以为决策者提供明确而具有说服力的论据。但值得注意的是任何一门科学都具有局限性,作为技术经济分析方法也不例外,因此我们又不能过于迷信它。因为技术经济分析活动往往都是在事情发生之前对其进行预测的分析及估价,因此带有明显的预测性。同时为了使运算成为可能,不可避免地对某些复杂的因素进行必要的简化。在时间上,有的研究对象所跨越的时间少则几年,多则十几年、几十年,在这样长的时间里,各种因素保持稳定不变,这不是一件人为可以控制的事情,当然不能百分之百的正确可靠。当分析的结果十分接近时,就不能拘泥于数学上的不等式概念来加以取舍了。
由以上可知,作为决策者,要通观全局。在众多的决策因素中,技术经济分析的结果、方案比较得出的结论固然是十分重要的因素,但并不是全部。因此我们要正确地认识它,适当地对待它,使这种科学的方法在设备综合管理中发挥其应有的作用。
