“ 假设检验是统计学中最重要的内容之一。”

统计学相关的内容，我们之前分享了《抽样分布》、《极大似然估计等参数估计》、《区间估计》等。参数估计与假设检验都属于统计推断的范畴，今天分享一下假设检验的基本知识。

01 为啥需要假设检验

正式开始之前，先聊聊，假设检验到底有啥用？

我们之前分享过《AB测试系统的搭建》相关的文章。假设我们实施了推荐算法的AB测试，回收效果数据后，将面临一个问题：改进后的算法，效果数据是否有显著提升？假设实施算法的改进之前，我们推荐模块的平均点击率是3%，方差是σ。实施算法后，测试数据的平均点击率是3.1%。请问，算法是否有明显的效果改善？

如果没学过假设检验，很多同学很有可能就会觉得明显改善了。因为3.1%比3%明显提升了嘛！但是学习了假设检验后，我们需要用更加严谨的思维来看待这个问题。3.1%的提升，有可能并不是算法优化带来的，而仅仅是系统误差而已。

可以说，假设检验是解决这一类问题的良药。因此在日常数据分析工作中，假设检验是很重要的内容与工具之一，应用场景比较多。

02 基本概念

先讲一下假设检验的一些基础概念。

（1）假设

对总体未知分布提出的论断，就是假设。这里的假设，是个名词。

其实在统计中，总体分布未知包括两种情况：一种是总体的分布类型未知，一种是总体分布类型已知但参数未知。

对于前一种（总体分布未知）提出的假设，属于非参数假设；对于后一种（分布已知参数未知）提出的假设，属于参数假设。

我们本篇文章重点是参数假设，非参数假设后面再详细展开。

（2）假设检验

什么是假设检验呢？

所谓的“假设检验”，就是检验假设成立与否的过程。它是用来判断样本与样本、样本与总体的差异是由抽样误差引起、还是本质差别造成的统计推断方法。

03 基本思想和步骤

如何进行假设检验呢？

（1）基本思想

我们通过一个通俗易懂的例子，来阐述假设检验的基本思想。

【例】比如一个袋子里有两种颜色（红、白）共100个球。张三说“一共有99个白球”。但是从袋子中抽取一个球，发现是红色的。那么张三的说法是对的吗？

【思想】用反证法。假设张三说的是对的，那么抽一个球是红球的概率是0.01，明显是个小概率事件，因此张三说的是对的这个假设，是很难成立的。因此我们有理由拒绝假设，那么，张三说的是错的。

（2）假设检验步骤

其实从上面的基本思想来看，基本也能get到假设检验的步骤。

步骤一：提出原假设H0与备择假设H1。

步骤二：假定H0成立，构造检验统计量T（需分布已知）

步骤三：给定α下，关注求解小概率事件的临界值

步骤四：根据样本数据，计算检验统计量T的值。

步骤五：根据T的值，判断小概率事件是否发生（即是否落在拒绝域中），下结论是否接受原假设H0

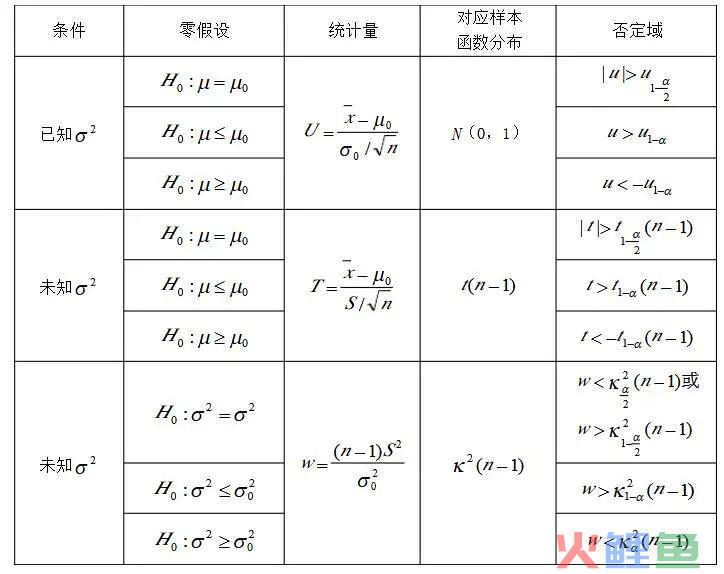
关于一个正态总体下，不同条件下的检验统计量的构造，可以参考下表：

是的，这里和区间估计中的枢轴变量是很像的。只不过区间估计时，枢轴变量中的参数是未知，用来求未知参数；而假设检验中，是假设未知参数已知，验证统计量是否属于小概率事件。

04 两类错误

我们前面说，根据实际问题提出假设，然后根据样本去检验假设是否成立。这是一个统计推断。步骤很严谨，但实际上做出的统计推断未必一定是对的。

为啥呢？

因为样本的随机性会导致错误，或者样本容量过小，也会导致推断是错的。因此，统计推断就是有误差的，这是正常的。

关于错误，分为了两类，可以看下表：

一类错误：即弃真错误，概率记为α。

二类错误：即取伪错误，概率记为β。

我们肯定期望将α和β的值越小越好，但现实中是不可能的，除非将样本量n无限增大。通常来讲，我们是尽可能确保α越小越好的前提下，再降低β。

关于假设检验，今天先分享这些，后面找机会结合具体案例给大家再分享。欢迎继续关注~

-END-