逻辑回归：基本算法原理及应用方法（不是回归的回归）

“ 逻辑回归，看似是回归算法，其实是典型与常用的分类算法。”

今天继续线性分类相关的内容，主要聊聊线性分类中的一个重要算法：逻辑回归。

01—逻辑回归基础

我们先介绍一下逻辑回归的一些基础背景。

（1）逻辑回归解决的问题

逻辑回归，虽然名字叫“回归”，但是它并不是用来回归的。什么是回归？我们之前有介绍过，回归问题解决的是因变量（即Y）是连续值的情况。

而逻辑回归是解决Y是离散变量的问题，即分类。

通常而言，逻辑回归主要解决的是二分类的问题，即分类的结果只有两个类别。比如【男，女】、【有钱，没钱】、【感染病毒，没感染病毒】、【垃圾邮件，不是垃圾邮件】……等等。

从上面的例子中，我们其实可以想象出，其实逻辑回归的应用场景是比较多的。比如基于邮件的特征，去判断一封邮件是否是垃圾邮件；基于用户行为，判断用户的性别等。

（2）都有哪些分类算法

上面我们提到了逻辑回归其实属于线性分类算法中的一种。

关于线性分类，主要有以下分类：

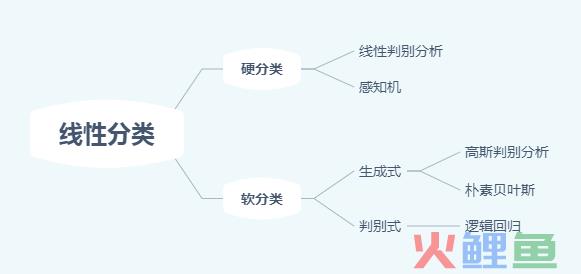
其中逻辑回归算法，属于判别式的线性分类模型——就是直接根据数据进行参数估计的模型，不需要使用贝叶斯公式。

而关于生成式的线性分类模型（主要就是朴素贝叶斯），我们后续专门进行分享。

（3）逻辑回归的本质

逻辑回归，虽然是一种分类算法，但确实和“回归”有一些关联。如果用一个公式表达：

逻辑回归=线性回归+sigmoid函数

对，这里的关键，就是sigmoid函数。这个函数就是我们之前讲回归和分类时候的激活函数。激活函数是为了将线性回归的连续性结果映射到离散值上，这样就是分类问题了。

至于逻辑回归算法的具体内容，我们看下面展开叙述。

02—算法逻辑

我们接下来讲一下逻辑回归算法的详细逻辑。

（1）sigmoid函数

上文中讲了，其实逻辑回归是线性回归的基础上，加了个sigmoid函数作为激活函数。那激活函数为什么是sigmoid函数呢？

我们先看一看下面的函数（单位越阶函数）作为激活函数：

这个是不是可以将连续的z（z=wx+b）映射到离散的y了？是的。

但是，如果将这个函数如果作为激活函数，将会导致函数是不连续不可导的。

因此，我们需要找到一个可以替代这个函数的函数，使其单调可微。什么函数呢？对，这就是sigmoid函数的一种：对数几率函数。

 

这个函数是连续的，极限取值是0-1，且可以按照0.5的阈值进行二分类。

用了这个函数以后，y和x的函数关系变为：

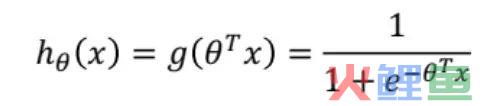
（2）损失函数

ok，既然有了上述的预测函数，下一步，我们要定义具体的损失函数。这里，我们通常用对数似然损失来作为损失函数：

 

 

这个公式比较好理解，就不展开了。

有了预测函数和损失函数，接下来就是进行参数估计的过程了。关于参数的求解，我们可以使用极大似然估计、梯度下降法等。

关于逻辑回归，今天主要分享这些内容，欢迎各位朋友继续关注~后续逐步分享贝叶斯分类、神经网络等机器学习算法。