中心极限定理——数据运营不得不学的统计学知识

中心极限定理（CLT）是指，给定足够大的样本量，无论变量在总体中的分布如何，变量均值的抽样分布都将近似于正态分布。

这是统计学中的一个基本定理，也是最重要的统计定理之一，是学习统计学绕不过的坎儿。不过好在这个概念实际上不难理解，看过下面这些例子，你也会觉得它其实蛮简单的。这些例子从反方面着手，我们很容易就能清楚地理解CLT了。

例1

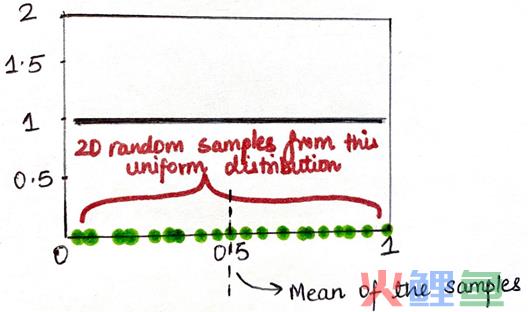
取一个均匀分布（从0到1，称为均匀分布，因为在0和1之间选择值的概率相等，因此它的概率密度函数(PDF)就是水平的黑色直线）。现在，假设从这个分布（绿点）中随机抽取20个样本，并计算这些样本的均值，最后得到一个值，在本例中，黑色点线表示0.5。

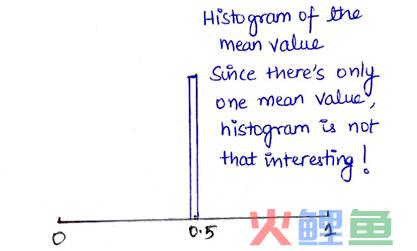
继续在直方图上绘制这个均值。因为此直方图目前只有一个均值，除此之外没有任何信息（下图1）。继续从相同的分布中随机抽取更多的样本，计算各自的均值并再次在直方图上绘制这些均值，便开始得到一个有趣的输出（下图2）。

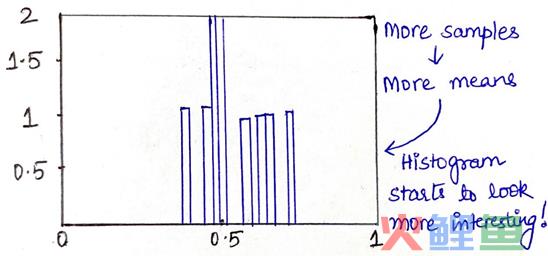
随着不断从均匀分布中随机取出越来越多的样本，并不断在直方图上绘制样本均值，我们可以得到一个正态分布的结果（右曲线）。

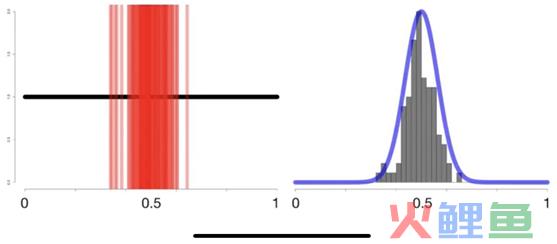
推论：从均匀数据分布开始，但是从中抽取的样本均值结果为正态分布。

例2

在第二例中进行与例1相同的步骤，唯一不同的是，这次将从指数分布中抽取样本。

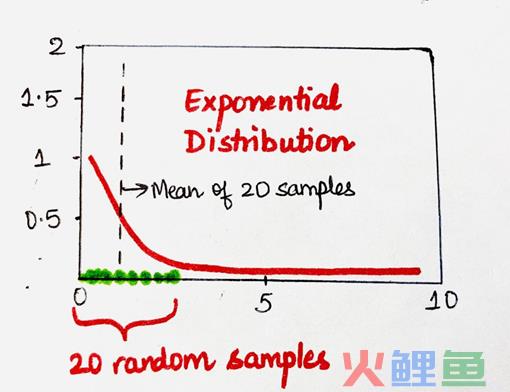
再次随机抽取20个样本，计算样本的均值，并将其绘制在直方图上。以此类推，在此指数数据分布中抽取大约100个样本，直方图如下所示。没错，样本的均值结果是正态分布！

推论：从指数数据分布开始，但从中抽取的样本均值为正态分布。

此时CLT的含义就变得非常直观了。它意味着，即使数据分布不是正态的，从中抽取的样本均值的分布也将是正态的。

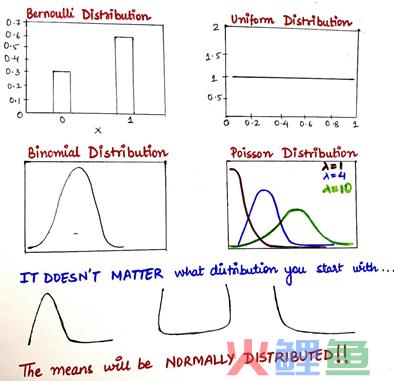
了解样本均值总是*呈正态分布有什么实际意义？

分析学领域从来少不了各种各样的数据，而源数据的分布我们不一定了解，但有了CLT，我们甚至不需要考虑这种情况，因为均值永远为正态分布，完全没有必要担心源数据的分布。

（注*-为了应用CLT，必须能够计算样本的均值。Cauchy分布没有样本均值，因此CLT不适用于该分布，但除了Cauchy，笔者没有遇到任何其他分布不适用于CLT的情况，因此，CLT可以适用于任何其他分布。）

图源：unsplash

我们能利用CLT作答还有很多：

· 可以利用均值的正态分布来确定置信区间。

· 在使用样本均值的情况下，可以进行任何统计检验。

· 可以进行t检验（即，利用两个样本的均值之间存在差异的特点）

· 可以进行方差分析测试（即，利用3个或3个以上样本的均值之间存在差异的特点）