ABtest的常用统计方法详解

在互联网公司的产品设计场景中，我们经常会遇到多个设计方案的选择。A/B测试比较产品的不同相关功能设计中哪个会导致更好效果。在A/B测试中，随机选择的一组用户显示产品的版本A，而另一组随机选择的用户显示版本B。然后比较测试结果以确定哪个版本的性能更好。A/B测试通常用于优化网站、应用程序和其他产品，以获得最大的效率。

例如，App或网页端某个页面的某个按钮的颜色是用蓝色还是红色，是放在左边还是右边？传统的解决方案通常是某位负责人拍板决定，但是从概率上，是很难保证传统的选择策略每次都是有效的，而ABTest显然是一种更加科学的方法，AB实验其实是对实验组A与对照组B做出的某种假设，计算两组差异是否存在统计意义上的显著性，最终根据显著结果做出判断。

举个例子，就是在一个功能点上现提出了两个方案，在评审中两种方案都各有支持者，比如某个页面的某个按钮的颜色是用蓝色还是红色，让一部分用户在进入到页面时网页呈现出来是蓝色按钮，另一部分用户在进入到页面时网页呈现出来是红色按钮，然后通过日志记录用户的使用情况，并通过结构化的日志数据分析相关指标，如点击率、转化是否成功等，从而对收集到的数据进行检验，看不同方案之间是否有显著性，并计算出哪个方案更符合预期设计目标，并最终将全部流量切换至符合目标的方案。

01.ABtest的几个步骤

步骤1：提出问题 (试验目的)；

猜想或假设 (实验假设)；

这个假设应该包括你想要改变什么，以及你猜测实验的方案有什么效果。

步骤2：设计实验 (试验设计)；

进行实验 (数据采集)；

AB测试的样本需要满足：随机与同质。

步骤3：分析数据 (数据分析)；

得出结论 (报告呈现)；

在通过检验后我们得到了方案之间是否具有显著差异性，还可以通过对各个方 案的数值进行统计，来查看哪个方案带来的效果更好。

02.ABtest的常用的方法：

本文主要是针对步骤3来介绍一下AB测试的检验方法，常见的包括独立样本T检验、单因素方差分析、卡方检验等等。

独立样本T检验

独立样本T检验用于检验两分组数据是否存在显著性差异。

举例：某电商平台，想提升用户客单价，运营部门做了两套方案：A、B激励方案，想小规模投放优惠给用户，测试下效果。

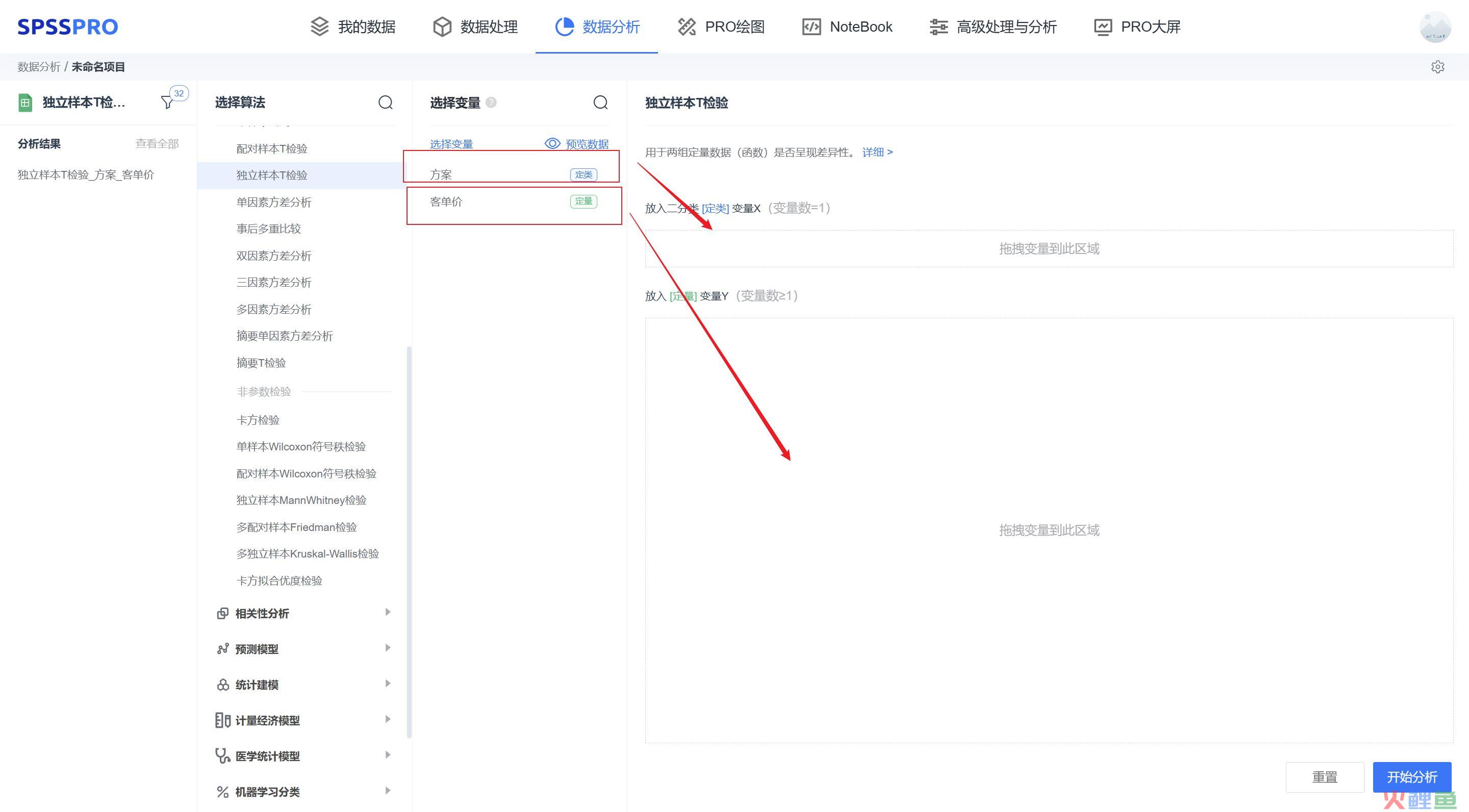
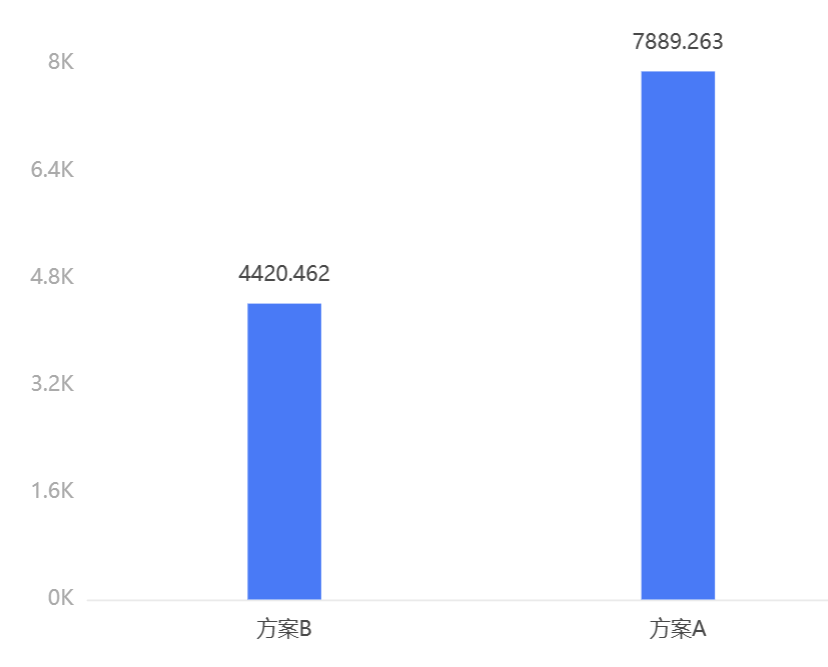
输出结果：独立样本T检验结果P值为0.000***≤0.05，因此统计结果显著，说明方案B、方案A在客单价上存在显著差异，其中，由两个方案的客单价均值柱形图可以看出，方案A效果比方案B好。

单因素方差分析

单因素方差分析用于检验不同分组数据是否存在显著性差异。

举例：某电商平台，想提升用户客单价，运营部门做了四套方案：A、B、C、D激励方案，想小规模投放优惠给用户，测试下效果。

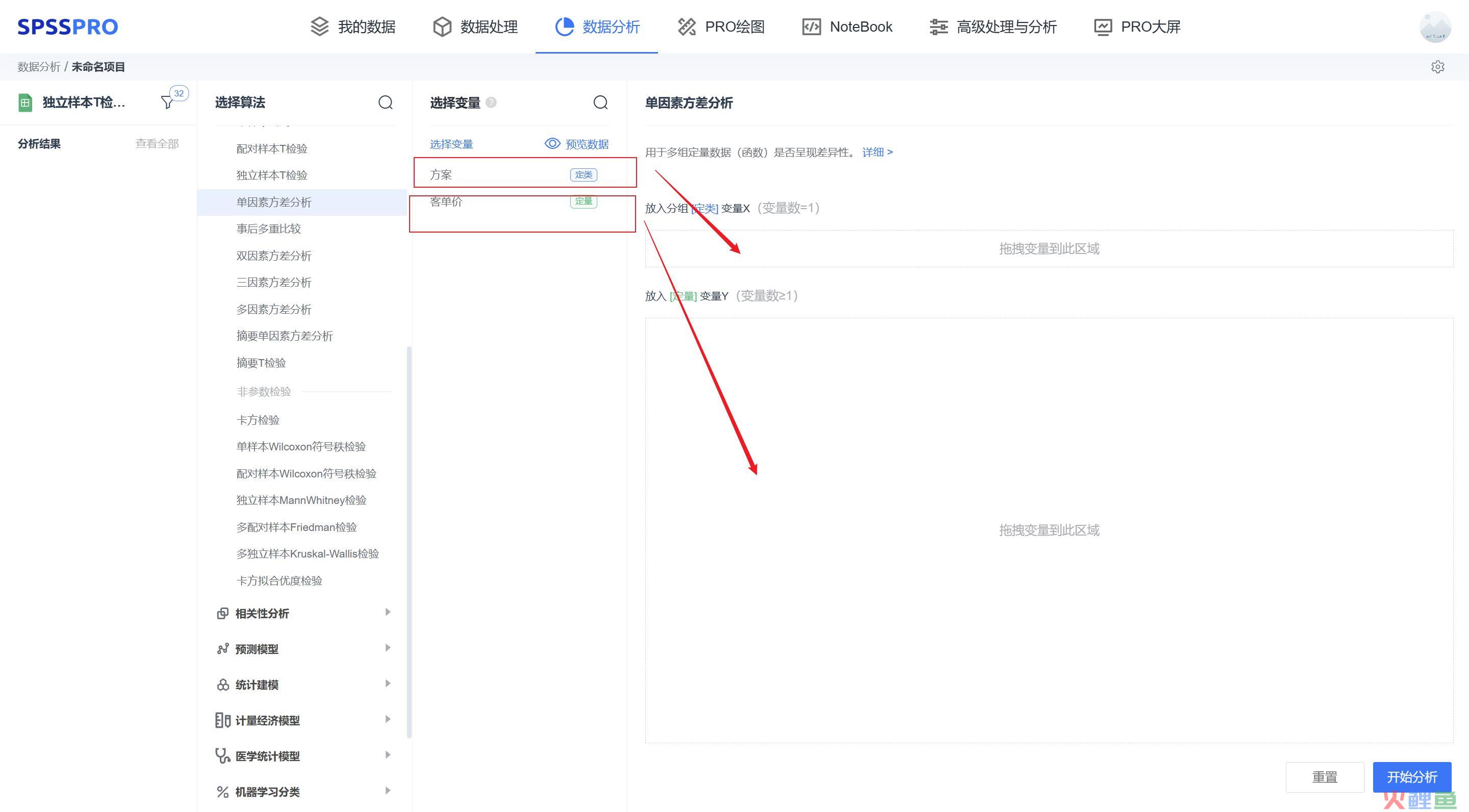
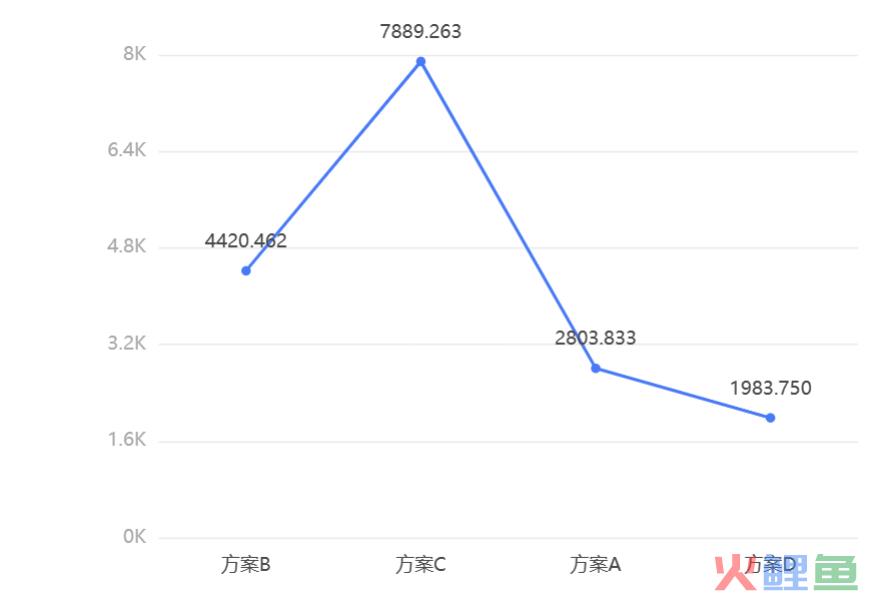
输出结果：单因素方差分析结果P值为0.000***≤0.05，因此统计结果显著，说明不同的方案在客单价上存在显著差异，其中，由各个方案的客单价均值折线图可以看出，方案C效果最好，其次是方案A。

卡方检验

卡方检验用于检验两分组变量是否存在显著性差异。

举例：某互联网公司，想要推广活动，设计部门做了两套网页营销方案A和B，哪个更有利于用户当天是否点击活动广告（0：未点击，1：点击）

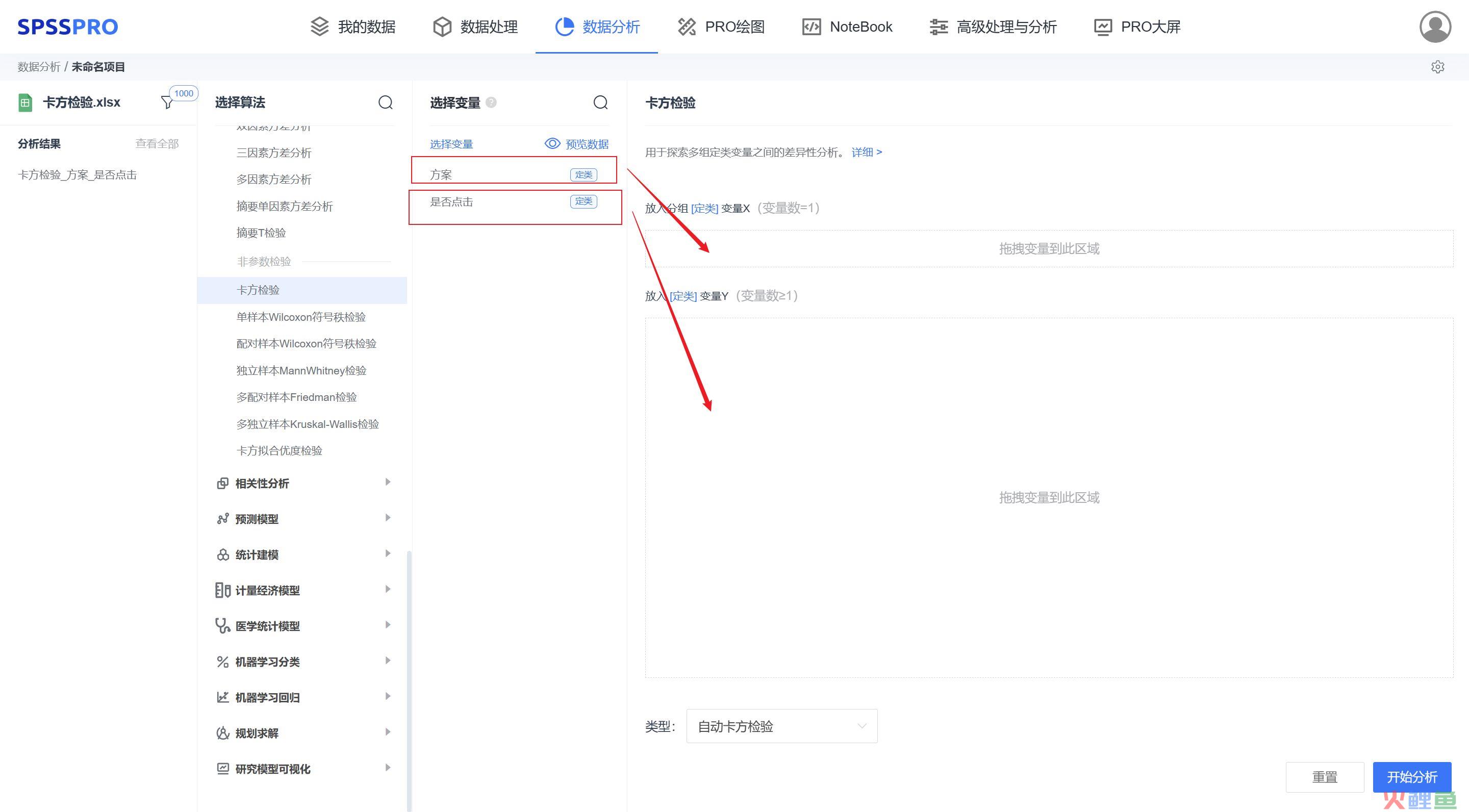
输出结果：显著性P值为0.005***，水平上呈现显著性，拒绝原假设，因此对于方案和是否点击数据存在显著性差异，并且方案A的点击率为130/500，方案B的点击率是171/500，说明方案B的转化率比方案A高。

02.ABtest的进阶方法

在用以上方法来做ABtest时，需要满足一个要求，两组用户是同质的，也就是用户属性是类似的。否则当两个用户群的量存在差异时，我们无法确定是策略变动导致，还是用户自身的原因。理想情况下，根据大数定理，只要是随机分组，在用户规模足够大的情况下，其他因素对结果的影响的平均效应是一致的，默认AB两组用户肯定是均匀分布的。但是实际应用中，很多应用场景的AB test能获得的样本比较少。比如想只在某个城市测试一个新的功能，或者产品本身用户较少，往往短期内能触达的在线用户有限，这种情况下两批样本用户本身属性差异有很大概率会很明显。

最传统的方法是将选中的几群同质用户（在用户属性上保持一致，例如城市，年龄等等），分别在几群同质有用户中按照随机的原则抽取部分样本到A组方案和B组方案）。AB测试需要切分流量到不同方案，如果不能正确切分，使得分到不同方案的用户群体特征分布一致，那么测试将没有任何意义。

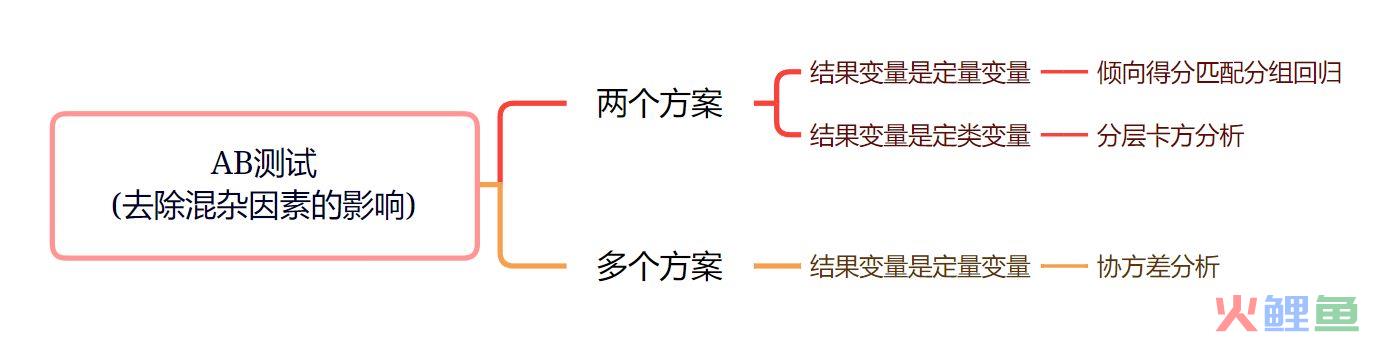
但是我们AB测试中，触达的在线用户有限，并不是全部用户都能触及到，就算是对其不同方案组样本进行均衡抽样，但也有可能会存在触达到功能的两批用户不同质，可以用去除混杂因素（用户属性数据）影响的方法来做这个方案对比的检验。根据方案的个数及结果变量为定量还是定类变量，推荐了以下几个方法，但是以下的方法具有一些自身的限制，需要根据要求来使用。

倾向得分匹配分组

在实际工作中，再怎样细致的分层抽样方案也不能保证实验组和对照组完全相似，把分层抽样方法的思路推演到极致，就产生了匹配的思想。既然担心实验组和对照组异质性，那么我们干脆对每一个实验组中的个体，在对照组中匹配一个与它很相似的个体，这样构造出来的对照组就与实验组非常接近了。

倾向得分匹配分组回归用于比较实验组与控制组的结果变量是否存在差异，它的原理是根据各个样本的倾向得分的距离来进行样本匹配，以每一个实验组为基准，在控制组内去寻找干扰变量尽可能相似的样本，以为了减少数据偏差和混杂因素的干扰。案例：某电商平台，想提升用户客单价，运营部门做了两套方案：A、B激励方案，想小规模投放优惠给用户，测试下效果。由于两个方案的关系是独立的，将方案A改为实验组（值为1），将方案B改为对照组（值为0）。其中方案A的响应人数有233个，方案B的响应人数有767个。

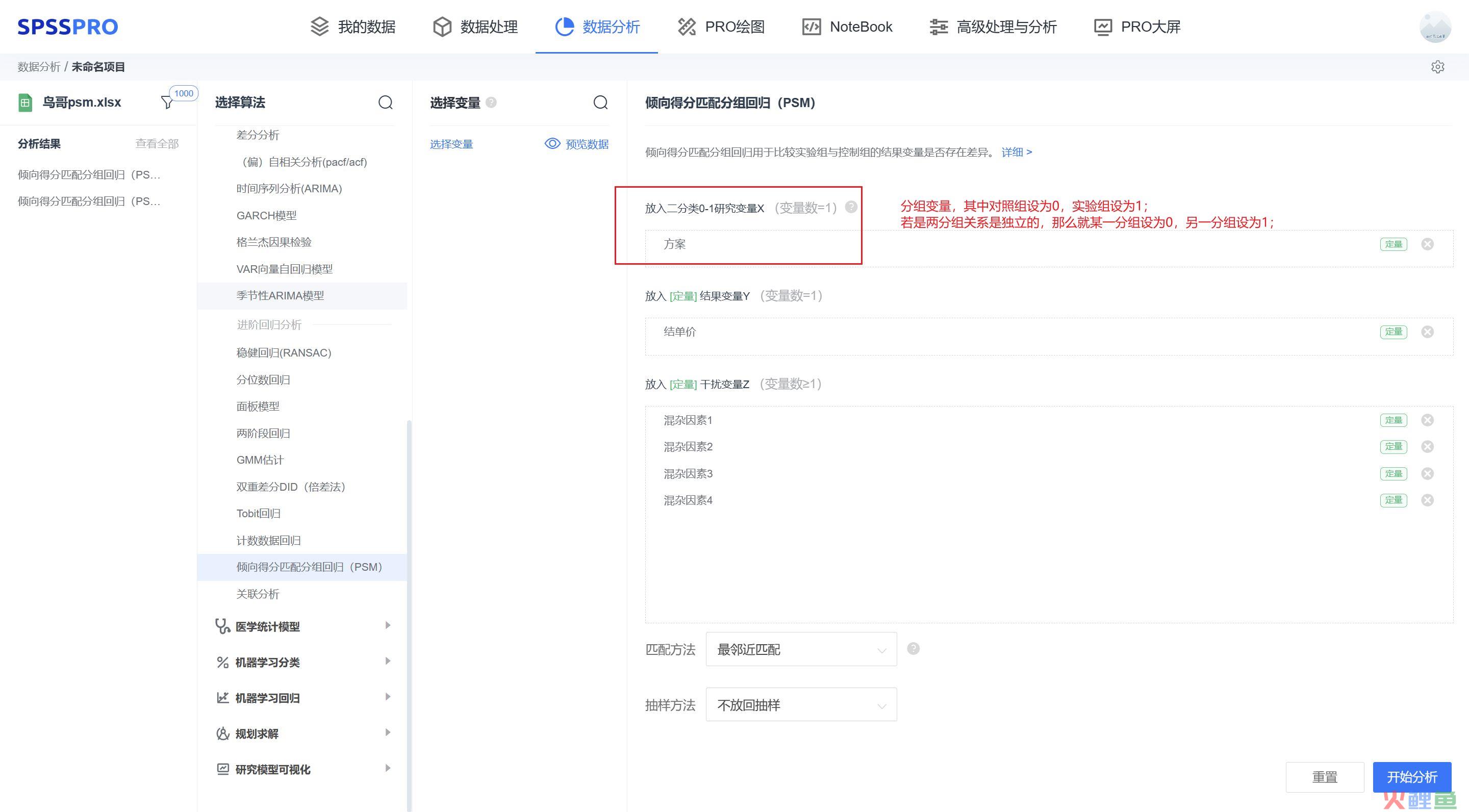
分析结果：

由上表可知，四个混杂变量在匹配前后标准化偏差减少 100%，并且都是”匹配前“T 检验有显著性(P0.05)，说明匹配效果极好。

上一步我们证明了匹配效果比较好，我们就可以继续用匹配后的样本来检验。所以主要是看匹配后的由 ATT 效应结果可知，匹配后数据的显著性 P 值为 0.000，呈现显著性，拒绝原假设，方案A和方案B在客单价存在显著性差异，其中实验组的客单价远远高于控制组，也即方案A的客单价远远高于方案B。

分层卡方分析

分层卡方是在卡方检验基础上，进一步考虑分层项的干扰（混杂因素）。但是分层卡方检验有较多的限制： 1、参与分析的混杂变量只允许有1个

仅支持 2×2×k 表格的数据结构（即卡方检验的两个分类变量均只允许有 2 个分类水平，混杂因素 Z 的 k 个水平是指任意水平，不做限制）。举例：某互联网公司，想要推广活动，设计部门做了两套网页营销方案，哪个更有利于用户当天是否点击活动广告（0：未点击，1：点击）

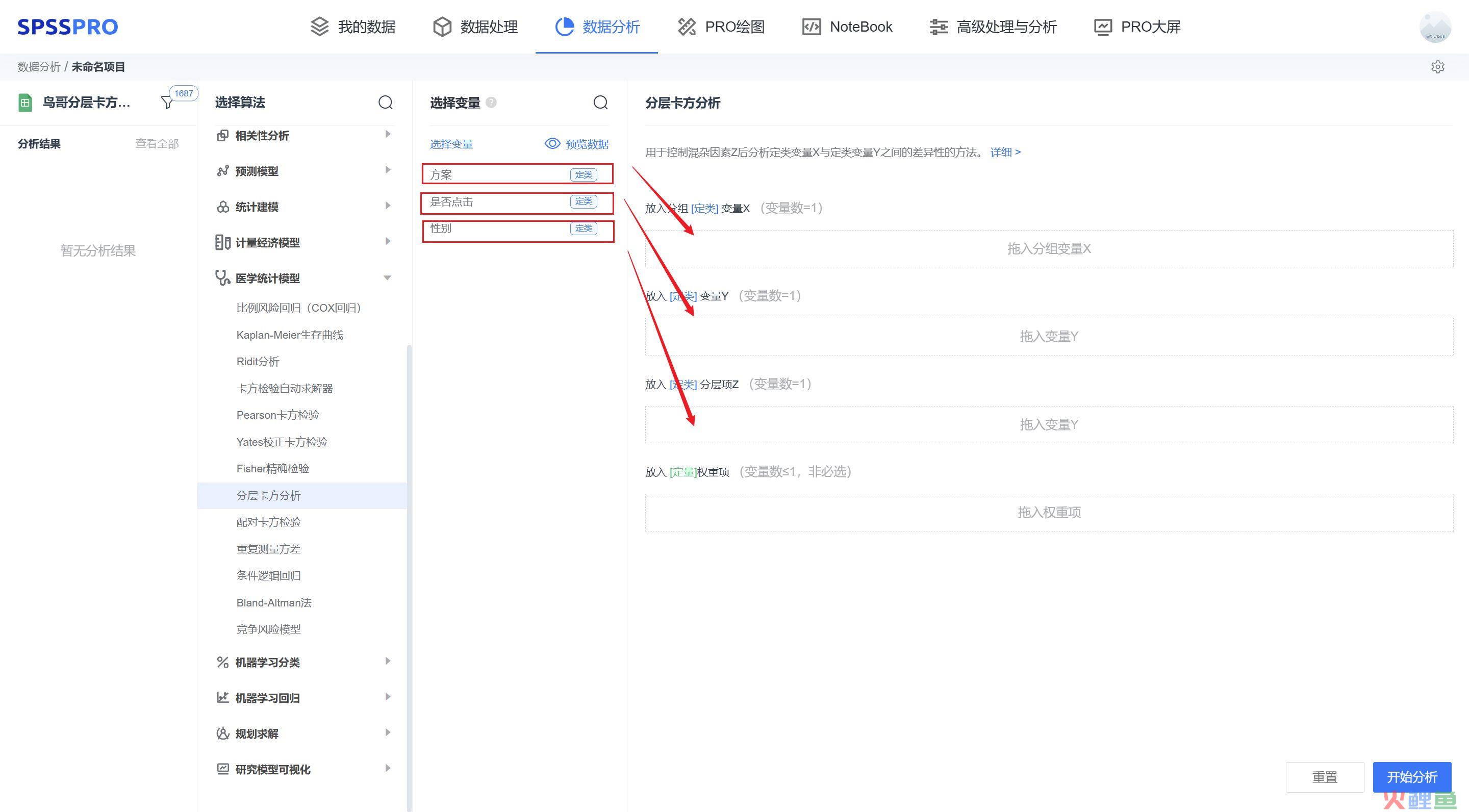
输出结果：

比值比齐性检验的显著性P值为0.970，不存在显著性，说明混杂因素各分类之间同质，并不存在混杂作用。单独进行分析，我们可以看到在女性中，方案2更受欢迎；在男性中，也是方案2更受欢迎。所以不管是男性还是女性，都是方案2更受欢迎。这也反映了性别并不存在并不对差异性结论存在影响。

在当比值比齐性认为混杂因素是的确起到干扰作用的时候，CMH条件独立性检验可以排除混杂因素得到卡方检验结果，显著性P值为0.000***，存在显著性，说明去除混杂因素影响后，是否点击和方案之间存在显著差异，即方案2总是比方案1更受欢迎。

协方差分析

协方差分析方法，可以排除在实验设计阶段无法人为掌控的因素对结果造成的影响。在统计分析阶段，将这些难以控制的随机变量作为协变量，在扣除协变量的影响后，再对修正的主效应进行方差分析，达到准确的分析评价控制变量对观察变量影响的目的。