数据分析必备：概率论基础知识

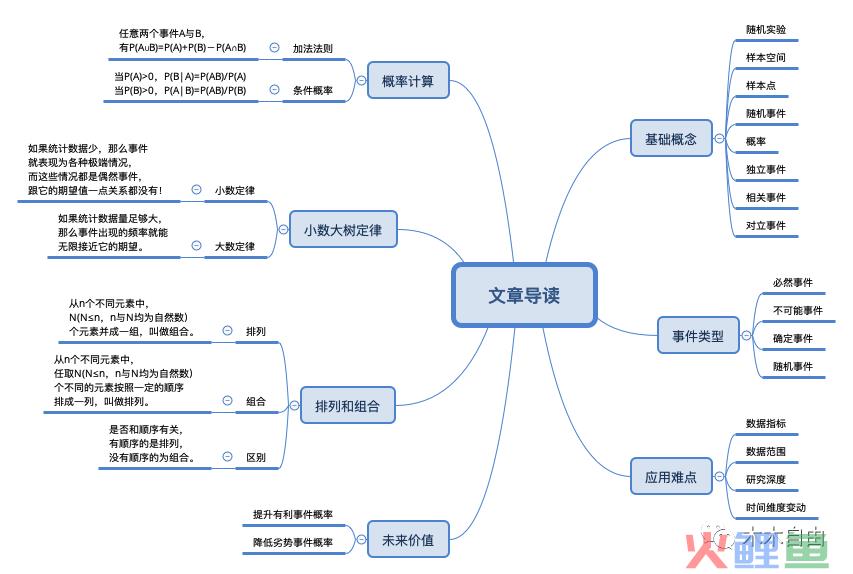
导读：从事数据分析的工作就不得不了解一些数学概念，而统计和概率可以说是打开数据分析大门的钥匙，将其所涉及的必备知识串起来，对于数据分析能力的进阶来说是重要的基石。

在我们短短的人生，会遇到很多人，经历很多事，看似随机的事件可不一定真的随机，冥冥之中自有定数的说法也不过是对无法解释的事件打一个定数的标签。遇到的人和经历的事都不是随机出现的。

一、基础概念

首先，我们先来梳理一下概率论的基础概念。

▌随机实验（E）

可以在相同的条件下重复地进行，每次实验的可能结果不止一个，并且事先明确知道实验的所有可能结果，每次试验将出现哪一个结果无法预知。例子：抛一枚硬币，观察正面，反面出现的情况。

▌样本空间(S)

随机试验所有可能的结果组成的集合。

▌样本点

样本空间的元素，即每个可能的结果。

▌随机事件

随机试验E的样本空间S的子集称为随机事件。

▌概率

在一定条件下，重复做n次试验，那么n次试验中事件A发生的次数，我们用nA来表示，如果随着n逐渐增大，频率nA/n逐渐稳定在某一数值p附近，则数值p称为事件A在该条件下发生的概率，记做P(A)=p。

▌独立事件

不受其他事件的影响的事件。

▌相关事件

受其他事件的影响。

▌对立事件

当一个事件发生，另一个事件一定不发生的事件。

二、事件类型

现在，来梳理一下事件的类型。

▌必然事件：

在条件S下，一定会发生的事件，叫做相对条件S的必然事件，简称必然事件。

必然事件发生的概率为1，但概率为1的事件不一定为必然事件。

▌不可能事件：

在条件S下，一定不可能发生的事件，叫做相对条件S的不可能事件，简称不可能事件。

人们通常用0来表示不可能事件发生的可能性。即：不可能事件的概率为0。但概率为0的事件不一定为不可能事件。

▌确定事件：

必然事件和不可能事件统称为相对条件S的确定事件，简称确定事件。

▌随机事件：

在随机试验中，可能出现也可能不出现、并在大量重复试验中具有某种规律性的事件叫做随机事件(简称事件)。随机事件通常用大写英文字母A、B、C等表示。

方便了解，我们把各类事件举例说明一下：

①必然事件：太阳每天从东方升起。

②不可能事件：太阳从西方升起。

③确定事件：平面上通过两点的直线只有一条。

④随机事件：明天下雨。

我们在生活中遇到的事件大部分都是随机事件，例如，明天的天气，过马路时的红绿灯，上班堵车的可能性等，但随机事件真的毫无规律吗？如果知道随机事件的有效范围，是否可以计算随机事件发生的概率呢？

三、排列和组合

那么，接下来看看什么是排列和组合呢？

排列和组合是确定随机事件有效范围的，也就是我们概念中的样本空间(S)。

有红球和黑球各5个，随机抓取2次（抓取后放回），得到的结果S={（红球，红球），（红球，黑球），（黑球，红球），（黑球，黑球）}4种，抓取一次的频数为1，结果为4个中的其中之一，所以任意一种事件发生的可能性（记为事件A）P（A）=1/4。

如果球的颜色有10种或者更多，那我们组合起来就比较费劲了，有没有公式可以利用？

关于排列与组合：有顺序的是排列，没有顺序的是组合。

▌组合：从n个不同元素中，任取N(N≤n，n与N均为自然数）个元素并成一组，叫做组合。

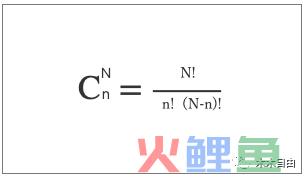
▌排列：从n个不同元素中，任取N(N≤n，n与N均为自然数）个不同的元素按照一定的顺序排成一列，叫做排列。

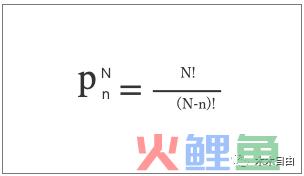
再次强调，排列和组合的区别在于，是否和顺序有关，有顺序的是排列，没有顺序的为组合。所以，事件（红球，黑球）、事件（黑球，红球）这2个在组合中是一个结果，在排列中就是两个结果。

四、概率计算

排列组合确定了随机范围（样本空间），那事件中的概率怎么计算呢？我们引入概率计算。

一个事件的概率是比较容易计算的，但现实情况是我们需要确定事件之间的关系，是互斥、独立还是相关？所以，我们需要引入一些概率的计算公式。

事件A和事件B有部分相同的交集，事件A的概率P(A），事件B的概率P(B)

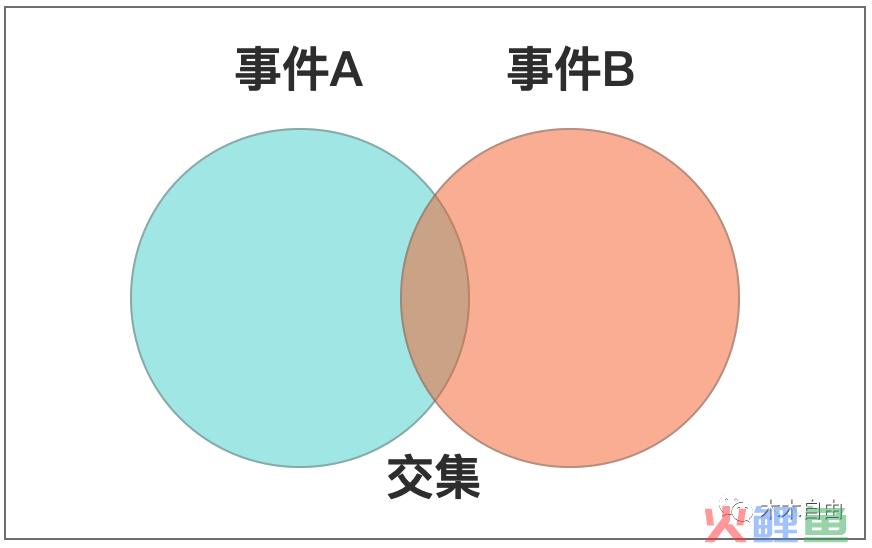
①加法法则：任意两个事件A与B，有P(A∪B)=P(A)+P(B)－P(A∩B)

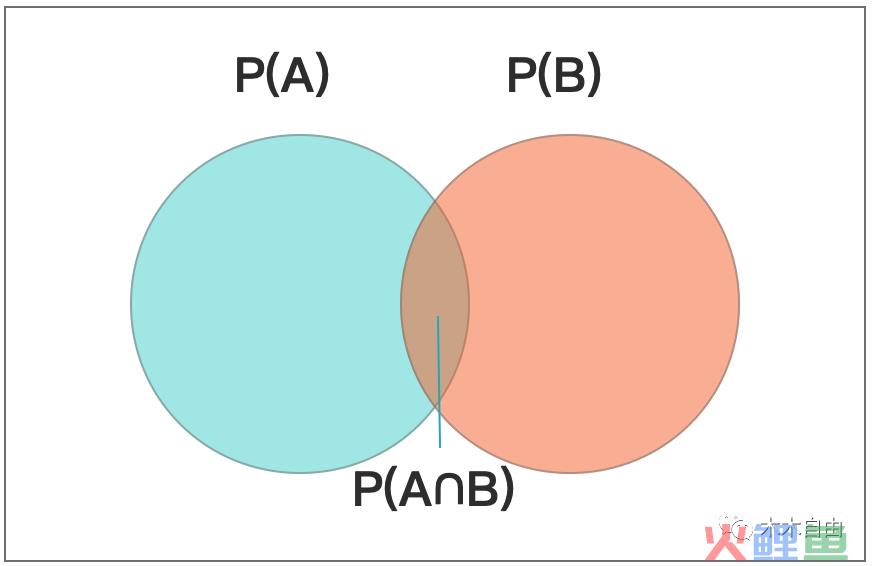
注：P(A)+P(B)很容易理解，为什么还要减一个P(A∩B)呢，因为图中的蓝色和橙色重叠的部分只有一个，P(A)+P(B)中多加了一份，所以需要减掉。

②条件概率：已知事件B出现的条件下A出现的概率，称为条件概率，记作：P(A|B)

当P(A)>0，P(B|A)=P(AB)/P(A)

当P(B)>0，P(A|B)=P(AB)/P(B)

注：条件概率的用途很多，例如商品转化率，回购率等，这些数据都很容易理解，但理论基础也不要忘记哦！

五、小数大数定律

在我们实际的生活工作中，会看到很多公司招聘要求本科学历，为什么不是高中生呢？对于企业来说，一个岗位的试错成本很高，高中生的适应性普遍没有本科生强（特例的请看小数定律），所以，企业的招聘也只是在大概率事件中获取部分结果而已。做一个选择题，二选一，如果你是老板，你选哪个？

A，高水平人群中挑一个

B，一般水平人群中挑一个

有句话说你遇见的人都是和你一般的水平，如果想要遇到比你优秀的人，那只有在更优秀的环境中去寻找那个人，所以，你当前的圈子，代表着你的水平，也不无道理。

我们一生中能遇到的人，只不过是在不断成长过程中形成的圈子里，随机遇到而已。越近的圈子中的概率就越大，越远的概率自然就越小，概率大不代表一定，概率小也不代表不可能。所以就存在，你不认识公司某个同事，却结交了一位八竿子打不着的网友。

以上的现象中，涉及了小数大数定律，那么，我们来看一下它们的概念。

▌小数定律（墨菲定律）：如果统计数据少，那么事件就表现为各种极端情况，而这些情况都是偶然事件，跟它的期望值一点关系都没有！

又例如，生孩子，一位母亲生了3个女孩，下一次生女孩的概率还是1/2，和前面生几个没关系；很多赌徒在输光了本金的情况下，还想继续赌下去，侥幸想都输了这么多次了，总该赢一次吧，这么想就错了，你前面输和赢与下一次的结果也是没有关系的。

▌大数定律：如果统计数据量足够大，那么事件出现的频率就能无限接近它的期望。但是数量足够多的时候，男孩和女孩的出生率越接近于1/2。

六、应用难点

在一个纸箱里放满了红、蓝颜色的小球抓出其中一个的概率，我们是能知道的。但是在一个事件中呢？我们所要收集的指标有多少？到什么程度？这个范围的边界怎么定义？是下图中的外边界还是内边界？

数据分析本质是挖掘数据并且根据数据得到并验证符合客观事实的分析结果，是在我们不知道的事件下对数据进行挖掘，发现、总结规律，毕竟已经知道的规律也已经没有了挖掘的价值，而时间维度对事件的影响也是至关重要的，所以数据挖掘面对的一直是一个未知的世界，需要我们不断的探索。

七、未来价值

总之，事件发生的概率是指在0和1之间的数值，1是一定发生，0是一定不发生，0和1之间是随机发生。我们所要做的就是在0和1之间寻找方案提升或降低事件发生的概率，并利用这一随机的概率达到我们的目的。例如，利用干预的手段提高种子发芽率，存活率，降低病菌感染率，病死率等等。

福利彩票中就大量运用了概率，利用少量的资金作为奖励刺激人们不断地去买入，并在此期间实现了不断盈利。现在的抽奖活动中也运用概率，并且很多商贩都把中奖率设置得极低，极少容易中奖，计算奖品的成本和中奖概率所带来的的盈利，以极高的利润率达到商业目的。

各类保险也是同样的，设定保险类型的时候已经调研出了保险事项发生的概率，全部的赔付金额只占了营收金额的极小部分。尽管如此，车险，人生意外险，重疾险，不买的人也不多吧，在总体人群中的事件概率是趋于期望值的，但对于个人来说，砸中你了就是100%。

那作为普通人的我们能否运用概率，达到另一个高度呢？

原文始发于微信公众号（Python数据科学）