等距抽样的估计

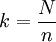
　　等距抽样又称为机械抽样或系统抽样，它是将总体各单位按某标志进行排序，然后按固定的间隔来抽取样本单位的抽样组织形式。根据需要抽取的样本单位数n和总体的单位数N，可以计算出等距抽样的间隔大小为

　　

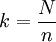
　　先从排序后序号为1，2，…，k的第一部分中随机抽出第i个单位，然后在序号为k+1，k+2，…，2k的第二部分中抽取第k+i个单位，再从序号为2k+1,2k+2,...,3k的第三部分中抽取第2k+i个单位，依此类推，最后从序号为(n-1)k+1,(n-1)k+2,...,nk的第n部分中抽取第(n-1)k+i个单位，一共n个单位构成样本。

　　总体排序标志由总体的有关辅助信息确定，与调查标志两者间可以有关也可以无关。如家计调查，按门牌号码排序就是无关标志排序，但是，如果选择的排序标志与实际调查标志间存在密切联系，要比无关标志排序的等距抽样更为优越。如农产量调查按平均亩产量高低排序，职工家计调查按平均工资多少进行排序，都可缩小各单位间的差异程度，有利于提高样本的代表性。

　　等距抽样的间隔应避免与现象本身的节奏性或循环周期相重合。例如，进行农作物调查时，抽样间隔就应避免与农作物垅长或间距相重合；进行工业产品质量调查时，产品抽样时间间隔不宜和上下班时间相一致，否则，就会因引起系统偏差而影响样本的代表性。

　　用等距抽样方式抽取一个样本后，就可以计算样本平均数。关键是这个平均数的平均误差如何确定，一般说来，排序后总体被分成n个部分，每一部分包含k个单位，从中随机抽取一个单位，其余单位情况未知，每一部分中的方差不可计算，一般也没有历史资料可以替代它们。因此，直接计算等距抽样的平均误差是有困难的，只能以间接方式计算其近似值，如果据以排序的标志与所要研究的目的没有关系，且第一个单位是随机抽取的，则等距抽样的平均误差就与随机抽样的平均误差相接近。为了方便起见，可以采用简单随机抽样的平均误差代替等距抽样平均误差

　　

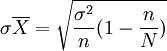
　　等距抽样一般都是无回置抽样，总体方差σ未知时，常用样本方差代替。

　　【例】某块麦地长300米，宽120米，包括120条垅，每垅长300米，现从这块麦地按等距抽样的方式，抽取50个2米长垅为样本进行实割实测。

　　样本距离为麦垅总长除以样本单位数，即300×120/50=720(米)：现从地角一边样本距离一半处抽取第一个样本单位，即从360米前后1米为第一个样本单位，以后每隔720米取一个样本单位，一直抽出50个样本单位为止。实测各样本单位产量如表所示:

表 各样本单位小麦产量 样本产量X(公斤)单位数nnX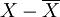 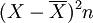0.864.8-0.40.96 11212-0.20.48 1.21416.800 1.41216.80.20.48 1.669.60.40.96 合计5060—2.88

　　试计算平均亩产量的抽样平均误差，并以95%的概率保证估计这块麦地的亩产量和总产量：

　　解：样本平均产量 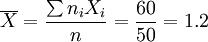(公斤)

　　样本单位标准差(公斤)

　　样本单位的抽样平均误差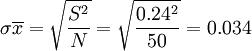(公斤)

　　这块麦地的面积是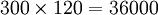：(平方米)，折合为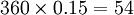(亩)。

　　由于样本单位垅长是2米，所以每亩含样本单位数是：

　　1/2×总垅长÷面积=1/2×36000/54≈333(个)。

　　平均亩产量=样本平均产量×每亩含样本单位数，即平均亩产量

　　1.2×18000/54=400(公斤)

　　平均亩产量的抽样平均误差=每亩含样本单位数×样本单位数的抽样平均误差，即为

　　18000/54×0.034=11.33(公斤)

　　由于概率保证是95%，即α = 0.05，则有Zα / 2 = 1.96。那么，亩产量的置信区间是

　　

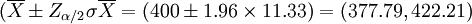
　　即亩产量估计在377.79公斤到422.21公斤之间。

　　总产量的置信区间是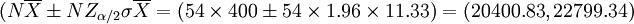

　　即以95％的概率保证，这块麦地的总产量估计在20401公斤到22799公斤之间。