凯利公式的概述

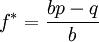
　　凯利公式是一条可应用在投资资金和赌注的公式。应用于多次的随机赌博游戏，资金的期望增长率最高，且永远不会导致完全损失所有资金的后果。它假设赌博可无限次进行，而且没有下注上下限。

　　

f = 现有资金应进行下次投注的比例 b = 赔率 p = 胜利机会 q = 输的机会 （一般等于 1-p ）

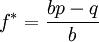
　　例如：若一个游戏有40%（p=0.40）机会胜出，赔率为2:1（b=2），这个赌客便应每次投注(2 × 0.40 -0.60)/2 = 10%的资金。

　　再举个最简单的例子：硬币的正反面，正面胜，反面输，胜率50%，赔率1.5:1。

　　代入凯利公式，b赔率是1.5，p和q都是0.5，则f=(bp - q) ÷ b = (1.5 * 50% - 50%) ÷ 1.5 = 16.6%。

　　f^*=16.6%是你下注最有利的比例，每次拿出16.6%进行下注，才能使你的收益最大化。 这是在你期望值为正的前提下，即（bp-q）>0，在抛硬币的案例里，期望值=0.25（赢面）是正的。

　　这条公式是克劳德·艾尔伍德·香农在贝尔实验室的同事物理学家约翰·拉里·凯利在1956年提出的。凯利的方法参考了香农关于长途电话线的嘈音的工作。凯利说明香农的信息论可应用于此：赌徒不必要获得完全的资讯。香农的另一位同事Edward O. Thorp应用这条公式在廿一点和股票市场上。1738年丹尼·伯努利曾提出等价的观点，可是伯努利的文章直到1954年才首次译成英语。不过对于只投资一次的人来说，应选择算术平均最高的投资组合。