模糊理论的主要研究领域
-
-
平凡的人生 这家伙很懒，还没有设置简介...
0 人点赞了该文章 · 20 浏览
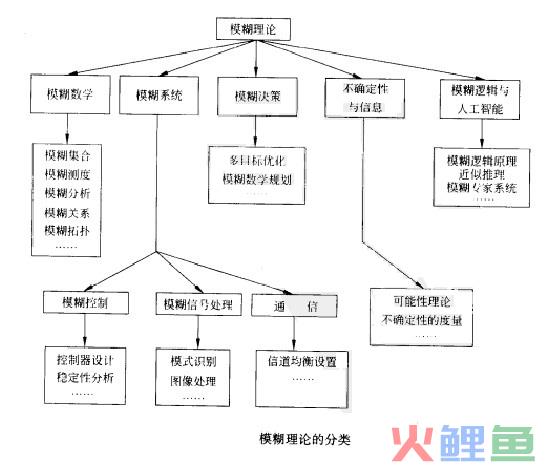
模糊理论是指用到了模糊集合的基本概念或连续隶属度函数的理论。根据下图可将模糊理论进行大致的分类。主要有五个分支：
(1)模糊数学，它用模糊集合取代经典集合从而扩展了经典数学中的概念；
(2模糊逻辑与人工智能，它引入了经典逻辑学中的近似推理，且在模糊信息和近似推理的基础上开发了专家系统；
(3)模糊系统，它包含了信号处理和通信中的模糊控制和模糊方法；
(4)不确定性和信息，它用于分析各种不确定性；
(5)模糊决策，它用软约束来考虑优化问题。
当然，这五个分支并不是完全独立的，他们之间有紧密的联系。例如，模糊控制就会用到模糊数学和模糊逻辑中的概念。
从实际应用的观点来看，模糊理论的应用大部分集中在模糊系统上，尤其集中在模糊控制上。也有一些模糊专家系统应用于医疗诊断和决策支持。由于模糊理论从理论和实践的角度看仍然是新生事物，所以我们期望，随着模糊领域的成熟，将会出现更多可靠的实际应用。
