机会约束规划模型的案例分析
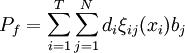
将风险发生概率Pf、风险后果概率Cf以及风险管理的费用作为随机因素处理,卜面给出这三个随机因素的详细描述:
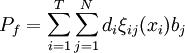 (1)
(1)
这里d_i是风险冈素i对风险发生的权重.bj是风险等级j的等级值.
ξij(xi)是为风险冈素i选择措施xi时风险发生处于等级j的概率.管理者在对风险控制措施作山选择之前,需要邀请数位专家对ξij(xi)进行预测,从而得剑一个最优的决策.然而,风险冈素的状态是不确定的,并且不同专家的预测结果也不尽相同,从这个角度来说,ξij(xi)不是一个确定的值。于是,把ξij(xi)作为随机变量来描述,由分布函数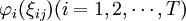 来近似专家们的预测.Xi是为风险因素f选择的控制措施,
来近似专家们的预测.Xi是为风险因素f选择的控制措施,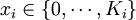
相似的,
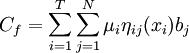 (2)
(2)
这里μi是风险后果因素i的权重;ηij(xi)是为风险因素i选择措施x_i时风险后果处于等级j的概率,它是一个随机变量,其分布函数近似为φi(ηij)。
风险管理的总费用表示为
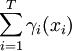 (3)
(3)
γi(xi))是风险因素i选择其措施xi的费用,为随机变量,与其对应的分布函数为Φi(γi),i=1,2,…,T。用于风险管理的总费用不能超过预算资金Cmax:
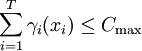 (4)
(4)
综上所述,风险管理的机会约束规划模型为
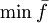 (5)
(5)
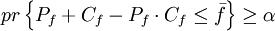 (6)
(6)
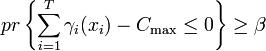 (7)。
(7)。
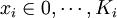 (8)
(8)
其中pr{·}表示{·}中的事件成立的概率.对于模型中的第1个约束(式(5)),多个目标值都可以满足它.在本问题中,要找出最小的,作为模型的目标值,即:
 (9)
(9)
式(9)是随机变量ξij和ηij的一个α悲观集,目标值 是满足该约束的值中最小的一个。可见,管理者对待风险的态度是十分谨慎的,即管理者是厌恶风险的。
是满足该约束的值中最小的一个。可见,管理者对待风险的态度是十分谨慎的,即管理者是厌恶风险的。
由于模型是一个带有随机变量的优化问题,考虑用蒙特卡洛模拟嵌入粒子群算法对问题进行求解。
