趋势外推法的案例分析

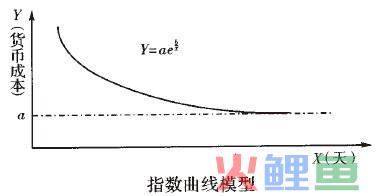
　　趋势外推函数很多，常用的有线性函数、抛物线函数、指数函数、修正指数函数、双曲线函数、罗古斯谛曲线函数、戈帕斯曲线函数及幂函数等。这里采用指数曲线模型预测法。

　　1.预测模型的建立

　　在一个较长的时期里，分规格分工部的标准可比成本应该呈下降趋势，并逐步逼近一个极限值。

　　因为这种标准可比成本实际上是由物耗直接得出，各时期比较的是物耗，所以随着生产技能的提高及生产设备的改进，生产定量的某种产品的物耗必然会降低，但是又不可能无限降低，所以长期来看应符合图。中曲线走向。

　　

　　上述曲线的方程Y = ae就是指数曲线模型.当a>0,b>0时,Y随X增大单调递减上凹,具有渐近线X=0和Y=a。当a>0,b<0时,Y单调递增;在X的区间(0,-2/b)上,曲线上凹,且当X→0时,Y=0;X=-2/b,Y = aexp( − b / 2)为曲线拐点坐标;在X的开区间(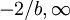)上,曲线下凹,且以Y=a为渐近线。其中a、b为参数。X是时间,可以天为单位,也可以周、月为单位,但必须统一(这里统一为天数)。为实际的综合成本或可比成本,我们用历史数据求出参数a、b确定模型,然后就可计算出趋势值Y_i。方法如下:将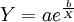化归为线性方程,两边取对数得:

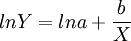　　（1）

　　令u = lnY,A = lna,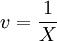,得：A+bv=u式(1)可看作是趋势外推法中的直线模型。直线模型的关键是如何确定a、b参数,使其误差最小。这里选用最小二乘法。

　　最小二乘法是使实际值和趋势值之差的平方和最小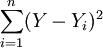：最小，即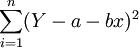为最小。(假设这里的Y就是u，即lnY；x是v，即1/X；要求的参数a、b就是对应的A、b)根据求最小值原理，对a、b求导数，并令其为零，即：

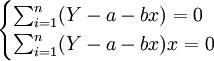　　(2)

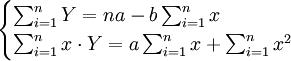　　(3)

　　n为时间序列的项数，解此联立方程，可求得a、b为：

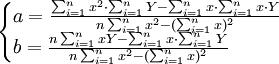　　(4)

　　以上计算a、b时，代表天数的x值为0，1，2，…，起点为0，计算比较复杂。为了简化计算，改变x值为…，-3，-2，-1，0，1，2，3，…；当天数为偶数时，用中间两天的中点为零，即x值为…，-5，-3，-1，1，3，5，…。由此可得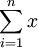总是为零。于是式（4）可简化为：

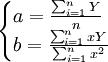　　(5)

　　上述计算完成后，在用相应的参数A、b替换a、b，然后带入解方程求出成本值。

　　2.程序流程

　　程序流程如下图所示。

　　

　　3.预测实例

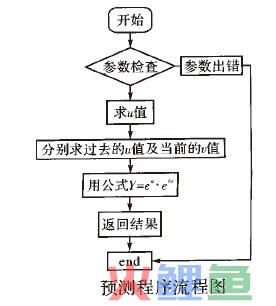
　　取某钢铁铸管集团公司在2001年六月份的日生产数据，如下表所示：

　　

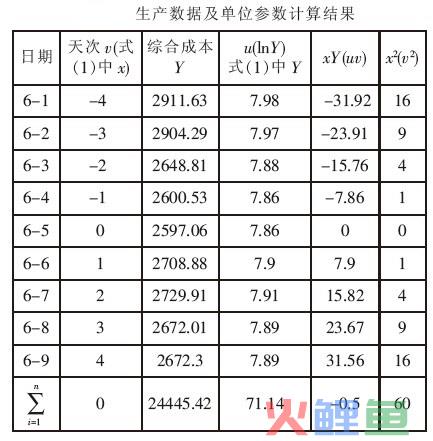
　　首先解出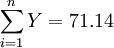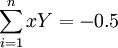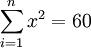，,,与n=9代入式（5）可得：

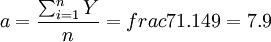　　(即是式（1）中的A)

　　

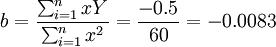
　　根据A的值及代换公式A = lna，可得a=2697.28,b不变，为方便起见v不代换。要预测6月10日的值，可带入公式：Y = 2697.28e − 0.0083v；6月10日的自变量v的值应该是5，因此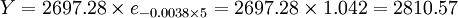，,实际上6月10日的综合成本是2718.15，误差是3.4%，预测结果比较准确。