灰色预测法案例分析
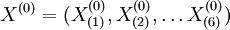
案例一:灰色预测法在百亚集团连锁企业的应用
商业连锁企业随着门店的不断增加,总部对企业的管理将变得越发困难,尤其是对销售量的预测,这严重影响了决策层对企业的控制和管理,影响总部的决策水平,包括资金的调度和使用、大批量进货以降低成本、门店的发展速度等等。随着模糊数学的不断发展,灰色预测方法得到了广泛应用,它对于商业连锁企业的销售管理,有指导价值。
一、灰色预测原理
灰色预测是灰色系统理论的重要组成部分,它利用连续的灰色微分模型,对系统的发展变化进行全面的观察分析,并做出长期预测。
灰色系统是部分信息已知、部分未知的系统。同时,灰色系统理论将随机过程看作是在一定范围内变化的与时间有关的灰色过程,将随机变量看成是在一定范围内变化的灰色量,显然,商品零售业就是一个灰色过程,商品销售系统就是一个灰色系统,销售量就是一个灰色量。
灰色系统理论认为,灰色系统的行为现象尽管是朦胧的,数据是杂乱的,但毕竟是有序的是有整体功能的,因而对变化过程可作科学预测。在灰色理论中,用来发掘这些规律的适当方式是数据生成,将杂乱的原始数据整理成规律性较强的生成数列,再通过一系列运算,就可以建立灰色理论中一阶单变量微分方程的模型即CM(1,1)模型。
下面根据百亚集团1995年至2000年门店分类商品销售额数据建立GM(1,1)模型,并预测百亚集团在今后几年里的门店分类销售额。
百亚集团门店历年商品分类平均销售状况表(单位10万元)。
年份199519961997199819992000 类别 食品类223.3227.3230.5238.1242.9251.1 烟酒类37.939.845.446.246.950.9 洗化类34.435.135.536.537.238.0 服针纺8.68.78.89.19.09.4 文娱类12.012.613.713.914.215.4 日杂类27.527.827.227.828.529.3二、模型的实际应用
据上表的原始数据列:
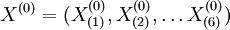
=(223.3,227.3,230.5,238.1,242.9,251.1)
作一次累加生成,得生成数列:
X = (223.3,450.6,681.1,919.2,1162.1,1413.2)
建立数据矩阵B及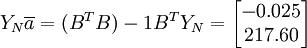
即a=-0.025 u=217.6 u/a=-8705.0
故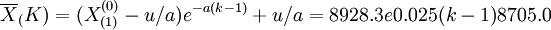 (1)
(1)
在该模型中,依次取K=1,2,3,4,5,6可以得到各生成数据的模型计算值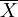 (1)及还原为原始数据的模型计算值X(0)。
(1)及还原为原始数据的模型计算值X(0)。
生成数对照表
序号123456 模型计算值223.3449.3681.7918.71162.31412.1 实际值223.4450.6681.1919.21162.11413.2还原数对照表
序号123456 年份199519961997199819992000 模型计算值223.3226232.4237243.6249.8 实际值223.3227.3230.5238.1242.9251.1 相对误差0-0.570.82-0.460.29-0.48从上面的经验可以看出a=-0.025,且接近于0,说明本系统采用灰色预测的方法是适合的,数据检验表明最大误差为0.82%,拟合精度较高。
令K=9,则X(2003)=2693万元
K=14,则X(2008)=3051万元
可以预测到2008年,百亚连锁店的门店食品类商品销量将达到3051万元左右,用同样的方法,可以求得百亚集团连锁店各类商品销售量的预测模型。
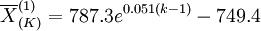 (2)
(2)
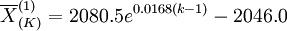 (3)
(3)
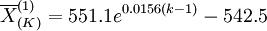 (4)
(4)
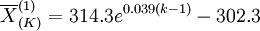 (5)
(5)
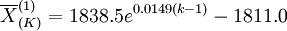 (6)
(6)
在上面的6个预测模型中所有的a<0,且接近于0,说明本系统采用灰色预测方法是适合的,拟合度应当较高。
代入上述预测模型,就可以预测到2003年以及2008年百亚连锁集团门店商品分类销售状况,这对于提高总部的商品批量进货决策、门店发展决策、资金的调度和使用以及规范化管理具有重要意义。
灰色预测法预测门店分类商品销售额(单位:10万元)
200120032008 食品类256.1269.3305.1 烟酒类53.158.875.9 洗化类38.439.543.1 服针纺9.59.710.4 文娱类15.316.419.9 日杂类29.730.633