抽样的基本术语

　　抽样已发展出了自己的一套专门术语，主要包括如下一些：

　　1、总体或抽样总体(population)

　　总体(population)通常与构成它的元素共同定义：总体是指构成它的所有元素的集合，而元素则是构成总体的最基本单位。在社会研究中，最常见的总体是由社会中的某些个人组成的，这些个人便是构成总体的元素。

　　比如，当我们开展对某省大学生的择业倾向进行研究和探讨时，该省所有在校大学生的集合就是我们研究的总体，而每一个在校大学生便是构成总体的元素。又比如，我们打算研究某城市居民的家庭生活质量，那么，该市所有的居民家庭就构成我们研究的总体，而其中的每一户家庭都是这个总体中的一个元素。

　　2、样本(sample)

　　样本与总体相对应，是指用来代表总体的单位，样本实际上是总体中某些单位的子集。样本不是总体，但它应代表总体，以抽样的标准就是让所选择的样本最大程度地代表总体。

　　3、抽样单位或抽样元素(sampling unit/element)

　　抽样单位或抽样元素是指收集信息的基本单位和进行分析的元素。在社会科学研究中，常用的抽样单位是个体的人，它也可以是一定类型的群体或组织，如家庭、公司、居委会、社区等。抽样单位与抽样元素有时是一致的，有时是不一致的。如在简单抽样中，它们是一致的，但在整群或多阶段抽样中，抽样单位是群体，而每个群体单位中又包含许多抽样元素。

　　4、抽样框(sampling frame)

　　抽样框又称做抽样范围，它指的是抽样过程中所使用的所有抽样单位的名单。比如，从一所中学的全体学生中，直接抽取200名学生作为样本。那么，这所中学全体学生的名单就是这次抽样的抽样框；如果是从这所中学的所有班级中抽取部分班级的学生作为调查的样本，那么，此时的抽样框就不再是全校学生的名单，而是全校所有班级的名单了。

　　5、参数值与统计值

　　参数值(parameter)也称总体值，是指反映总体中某变量的特征值。例如某地所有职工的平均收入水平和总体收入等都是参数值。但参数值多是理论值，难以具体确定。通常是根据样本的统计值来推论总体的参数值。

　　统计值（dstatistic）也称样本值，是指对样本中某变量特征的描述。它通常是实际统计分析的数值。例如，根据某一样本资料可计算其平均收入水平、构成比例等。用样本统值去推论参数值时，二者是一一对应的。下表列出了常见的一些特征值：

参数值统计值 定义反映总体特征的指标反映样本特征的指标 特征值N (总体数)μ(总体均值)σ(总体标准差)P(总体成数)n(样本数)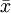(样本均值)s(样本标准差)p(样本成数)

　　6、抽样误差(sampling error)

　　样本统计值与所要推论的总体参数值之间的均差值就称为抽样误差。这是由抽样本身产生的误差，它反映的是样本对总体的表性程度，故又称代表性误差。我们在下面将结合样本数的确定再做具体讨论。

　　7、置信水平与置信区间(confidence 1evel and interval)

　　置信水平和置信区间是与抽样误差密切相关的两个概念。置信水平，又称置信度，是指总体参数值落在某一区间内的概率。

　　而置信区间是指在某一置信水平下，用样本统计值推论总体参数值的范围。其大小与误差密切相关，置信区间越大，误差也越大。