37%法则的数学过程
-
-
guiyang95 这家伙很懒，还没有设置简介...
0 人点赞了该文章 · 42 浏览
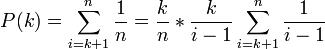
假设这片玉米地有N个玉米，数学模型上说，就是先拒掉前面 k 个玉米，不管这些玉米有多大；然后从第 k+1 个玉米开始，一旦看到比之前所有玉米都要大的，就毫不犹豫地选择它。不难看出，k 的取值很讲究，太小了达不到试的效果，太大了又会导致真正可选的余地不多了。这就变成了一个纯数学问题：在玉米总数 n 已知的情况下，当 k 等于何值时，按上述策略选中最大玉米的概率最大？
如何求出最优的 k 值？对于某个固定的 k，如果最适合的玉米出现在了第 i 个位置，k的概率记作P(k)。
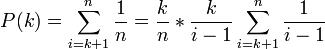
用 x 来表示 k/n 的值，并且假设 n 充分大，则上述公式可以写成：
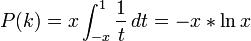
对 -x · ln x 求导，并令这个导数为 0，可以解出 x 的最优值，它就是欧拉研究的神秘常数的倒数—— 1/e
由于 1/e 大约等于 0.37（e ≈2.718281828459），因此这条法则也叫做 37% 法则。
