“ 参数估计是统计学的重要内容。”

之前的文章《总体、样本与统计量》、《卡方分布、t分布与F分布》等介绍了统计学的一些基础知识，今天分享一下关于参数估计的基本概念。尤其是极大似然估计，有着重要的应用。

01—参数估计的定义

首先，什么是参数估计呢？

之前我们其实已经了解到很多种分布类型了，比如正态分布、均匀分布、泊松分布等。拿正态分布举例，决定正态分布的有两个参数：均值和方差。因此，参数就是决定分布的关键性数据。知道了参数，也就是知道了分布的详细内容。

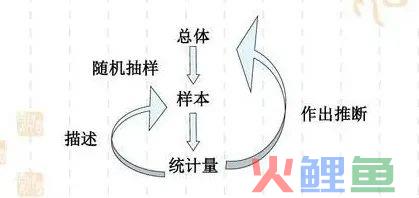
问题来了，总体的分布类别如果我们知道了，是不是只要知道分布的参数，就能知道总体的分布详情？是的。那如何能知道总体分布的参数数值呢？这就是参数估计。即，用样本的数据来构造函数（即统计量），来估计总体参数，这就是参数估计。

上图就是用样本统计量估计总体的过程。这也是统计学的重要意义之一。

02—点估计和区间估计

首先，什么是点估计和区间估计？

点估计就是用一个数值对对总体参数给出估计；而区间估计是在点估计基础上，给定一个具体的估计范围。

例如，估计中国全部人口的平均身高。161cm就是一个点估计，150cm~173cm就是一个区间估计。

区间估计和置信度相绑定。即估计的区间覆盖真实参数的概率。

常用的区间估计和点估计方法见下图：

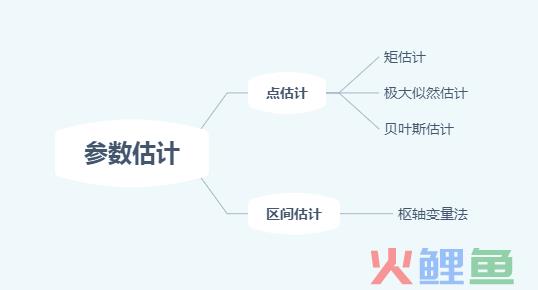
其中矩估计、极大似然估计在下文中展开。区间估计下次分析。

03—矩估计法

什么是矩估计呢？

矩估计比较好理解，就是用样本的矩直接作为总体矩的估计值。啥意思呢？就是我们将样本的矩计算出来，直接作为总体的矩即可。

当然，这里的阶数要保持一致。及样本的一阶矩估计总体一阶矩，样本二阶矩估计总体的二阶矩……

从以上定义中也可以看出来，矩估计法是一种点估计的方法。

04—极大似然估计法

极大似然估计，是另一种点估计方法，也是机器学习等学科中经常使用到的方法。简直就是重中之重。

（1）基本定义

定义：使样本事件发生概率最大的参数值，作为总体参数的估计值，就是极大似然估计。

怎么理解呢？举个例子。

比如箱子中有100个球，共两种颜色白和黑。已知白球和黑球的比例是1:99（但不知道谁是1）。目标是估计箱子中什么颜色是99个。随机抽取一个球，发现是白球。那么从直观上讲，是不是大概率箱子中是99个白球？当然也有可能箱子中是99个黑球，正好有1个白球还正好被抽到了。但是明显这种情况概率较小。

上面这个例子，就是极大似然估计的过程。选择的是概率最大的参数。

（2）极大似然估计的应用过程

极大似然估计的应用方法，通常遵循以下步骤：

步骤一：写出总体的概率/密度函数

当总体是离散型变量时，写的是概率函数；当总体是连续型函数时，写的是密度函数。

步骤二：写出似然函数

构造似然函数如下：

从上面的公式中，其实就是将每个样本观测值带入总体概率函数中，求所有样本的概率连乘。这个连乘，就是关于总体参数的一个似然函数。

似然函数有了，下面，我们的目标就是求使得该函数取最大值时的参数值，这个参数值就将作为一个总体参数的极大似然估计。

步骤三：两边取ln

由于通常似然函数都是连乘的形式，不容易取到最值，因此采用取ln的方式，将连乘变形为加法。

步骤四：两边求导，令导数=0，求参数

通常情况下，最值都是在导数为0的地方取到，这里令导数=0，求参数。即此时的参数值，使得导数为0，取得整体似然函数的最大值。即，此时的参数值是整体参数的极大似然估计。

当然，如果是多个参数的情况下，这里则分别对每个参数求偏导数，令偏导数为0，分别求各个参数的极大似然估计。

05—点估计优良性的判断准则

上面我们讲到的两种点估计方法。那如何判断一个点估计是好还是坏呢？这就是点估计的优良性判断，主要有以下3个准则：无偏性、有效性、相合性（一致性）。

（1）无偏性

无偏性的含义是：用样本估计的参数值的期望，等于真实值。

这个其实很好理解。我们进行参数估计不就是为了尽可能“猜”出总体参数的数值嘛，如果连期望都不相等，那岂不是基本就估计错了么……

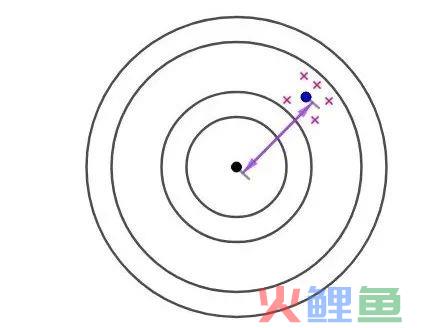
上图就是样本的期望明显和靶心（总体参数）有系统性偏差，显然不是好的估计。

因此，无偏估计是要明显好于有偏估计的。有以下 结论：

样本均值是总体均值的无偏估计

样本方差是总体方差的无偏估计（修正后的，分母是n-1。对，就是为了使得样本方差是无偏的。未修正的，就是有偏估计）

（2）有效性

有效性的含义是：用样本估计的参数值的方差，如果越小，就越有效。

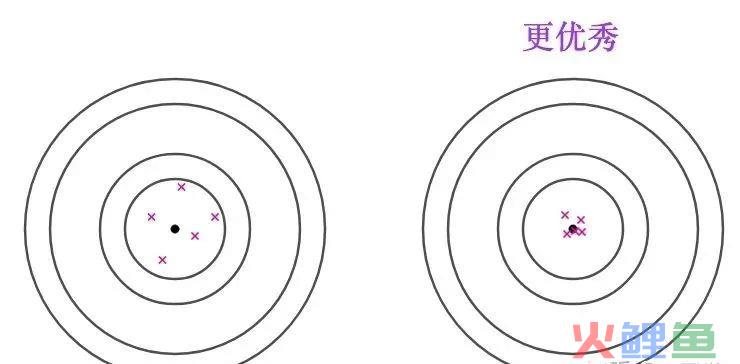
上图就比较清楚的反映了。两个估计都是无偏的，但是第二个估计明显更集中，方差更小，因此效果也就更好。因为更加容易和真实值（即总体参数）相近。

因此，对于多个估计，如果都是无偏的，我们优先选择有效性更强的作为总体的估计。

（3）相合性（一致性）

相合性的含义是：当样本量越来越大的时候，估计值和真实值的距离越来越小。

这个比较好理解，就不展开了。

关于参数估计、极大似然估计等，今天分享到这里，欢迎继续关注~

-END-