概率盘法的案例分析

案例一：石油价格的概率盘法

　　例如，某公司的利润和原油价格有较大关系，现想预计今后五年中，原油价格涨、低、平稳的概率。假定现在的价格是30元栏，且设五年内不会有石油禁运发生。为了获得这一主观概率，决策人询问一个石油经销商。

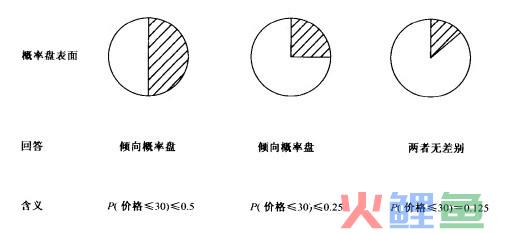
　　首先把概率盘上的黑白区域调整为相等，然后问被测人，是愿意打赌——“概率盘上的指针落在黑色区域”，还是打赌——“在五年内石油的价格低于30元”。假定被测人认为概率盘上的指针落在黑色区的可能性大，(也就是说他愿意在概率盘上打赌)。那么决策人把黑色区缩小，比如缩到1／4面积，再询问被测人，在这种情况下，他愿意打哪一个赌——是概率盘上的指针落在黑色区域上的赌，还是认为五年内石油价格低于30元。

　　如果被测人仍认为指针落在黑色区(现为1／4圆盘面积)的可能性大。则再缩小黑色区，比如1／8圆盘面积，再问被测人。这一回被测人可能会说：“好了，我现在既不愿意在概率盘上赌搏，也不愿意赌石油价格在五年内会在30元以下，我觉得这两种赌博有相同的结果。”

　　这样我们就可认为石油价格低于30元的概率是0．125(1／8圆盘的面积)。上面的询问过程可用下图表示。下一步再提出一个新的问题。

　　如石油价格是否会高于32元，进行与上面相同的询问。假定石油价格高于32元的推测与概率盘黑色区域占1／2的可能性相等，这时可认为价格高于32元的概率是0．5。

　　那么价格在30—32元之间的可能性就是1 - 0．5 - 0．125=0．375。

　　当然还可以对这最后的结论进行检查，也就是将概率撤十的黑色区调整为整个面积为0．375，然后问被测人，他是否认为指针落在黑色区域的可能性，与石油价格在30—32元的可能性相等。如果被测人认为是相等的，则试验中止，如认为是不等的，则要从头开始，重复以前的试验，以便找出不相吻合的原因。

　　如果测出的概率总和不等于1，但很接近，这时可以把数据正常化，即把每个预测值被总和除，得到概率值。