本量利分析扩展

　　前面本量利分析中假设收入和成本都呈线性，在盈亏临界点和保利点分析时，也假设销售单价、单位变动成本和销售量等因素也是确定的。而在现实经济生活中，情况可能复杂得多，如收入和成本可能不呈线性，某些因素在未来期间的状况不能确定等。本节就是在这样一些复杂条件下，来进行本量利分析。

一、非线性条件下的本量利分析

　　在非线性条件下，总收入或总成本随业务量的增长而呈曲线增长时，就可能应用非线性回归。非线性回归分析中最常用的方程式是：y=a+bx+cx2。企业可以根据销售量、销售额和成本等历史数据，计算出非线性回归方程的系数，然后分别计算一阶和二阶导数，以分别求出盈亏临界点和预计目标利润。

　　【例-8】某公司只生产和销售单一产品，而且产销平衡。会计人员对过去销售量、销售额和成本数据的分析，发现总成本和销售量、总收入和销售量均为非线性关系，进行回归分析后，确定了总成本和总收入的非线性回归方程，分别是：

　　总成本方程：TC=0.005x2-4x+2400

　　总收入方程：TR=8x -0.007x2

　　求该公司的盈亏临界点.利润最大化下的销售量和最大利润.最优售价。

　　式中：TC——总收入

　　　　　TR——总成本

　　　　　 x——产销量

　　利润（P）=TR-TC=（8x -0.007x2）-（ 0.005x2-4x+2400）=-0.012 x2+12x-2400

　　1．求盈亏临界点

　　令P=0，即：-0.012 x2+12x-2400=0，可以得到盈亏临界点：

　　解得：x1=723（台）

　　　　 x2=276（台）

　　也就是说，总收入线和总成本线有两交点，即两个盈亏临界点，分别对应的销售量是723件和276件。

　　这一现象可以通过下图来表示：

　　

　　　　　　　　　　　图-4 非线性关系下的盈亏临界图

　　2．求利润最大化的销售量和最大利润

　　由于P=-0.012 x2+12x-2400，所以可以求出x的一阶导数Px′，当Px′=0时，可实现利润最大化，即Px′=（-0.012 x2+12x-2400）′=-0.024x+12

　　令Px′=0，则有x=500（台）

　　也就是说，产量达到500台时，企业实现最大利润，此时的利润=600（万元）

　　3．最优售价：

　　在x=750台时，企业的总收入（TR）=8x -0.007x2=8×500-0.007×5002=2250（万元）

　　此时的产品售价=TR/x=2250÷500=4.5（万元/台）

　　在成本与销售量.收入与销售量呈非线性的条件下，企业制定生产计划和营销政策时，不能以产销量最大化为目标，而应以利润最大化作为经营目标，以此来确定最优产销售量和最优售价。

二、不确定情况下的本量利分析

　　我们知道，利润受到销售价格、销售数量、单位变动成本和固定成本等因素的影响。这些因素的变动必然引起利润的变动。如果这些因素的未来变动情况可以确定，如销售价格由现在的多少元提高或降低到多少元，单位变动成本将来会提高或降低到多少元，等等，那么，利润由此增加或减少的数值也就可以确定。但在实际经济生活中，销售价格、销售数量、单位变动成本和固定成本因素的未来变动情况受多种因素影响，对它们未来变动情况的估计往往很难十分准确，只能粗略的估计，也就是只能估计它们的变动范围，以及有关数值在这个范围内出现的可能性（概率）是多少。这样，对利润变动的预测值必将有多种可能。可见，对于不确定情况下的本量利分析，首先要确定影响利润的各因素的各种可能值，然后计算各因素可能值的每一种组合下的盈亏临界点或目标利润。最后，再以各种组合下的组合概率为权数计算盈亏临界点或目标利润的组合期望值，最终计算出各期望值的合计数，也就是盈亏临界点或目标利润的预测值。

　　（一）不确定情况下的盈亏临界点分析

　　【例-9】某企业只生产和销售一种产品。经过对影响售价、单位变动成本和固定成本的各因素的考察分析，估计出未来年度销售单价、单位变动成本和固定成本的数值和相应的概率如表-2所示：

　　表-2

销售单价单位变动成本固定成本 估计值概率估计值概率估计值概率 2000.71200.8400000.9 1900.31180.2450000.1

　　根据该表资料，可以预测出盈亏临界点。具体计算过程如表-3所示。

　　

　　从上表可以看出，单价、单位变动成本和固定成本三个因素都有两种可能出现的结果，这样，盈亏临界点就有8种可能出现的结果。以每一种盈亏临界点的结果乘以与这种结果相对应的组合概率，就可以得到该组合下的期望值。8种组合下期望值的合计数就是盈亏临界点的销售量的预测数525件。

　　可见，在预测未来的盈亏临界点时，如果能把影响盈亏临界点的各因素未来可能发生的各种结果都考虑进去，将会更加接近客观实际。

　　（二）不确定情况下的利润分析

　　【例-10】假定上例中该企业预计未来年度一定会销售4000件产品（此时概率为1），则未来年度预计目标利润的计算过程如下表所示。

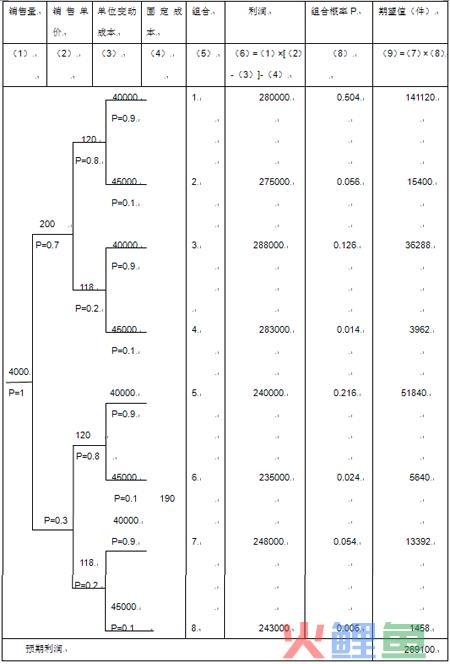
　　在不确定情况下预测利润，其方法与前面预测盈亏临界点的方法基本相同。本例中如果销售量也有多种可能值，就需要分别确定各种销售量情况下的利润值。此时，各种组合的数量会更大，利润预测也会变得更加复杂。