二次曲线法的计算
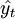
用最小二乘法确定待定参数
1) 参数的确定
设yt表示第t期的时间序列的观察值;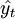 ——第t期的预测值;et——第t期的离差;Q——离差平方和。由二次曲线外推预测法的模型
——第t期的预测值;et——第t期的离差;Q——离差平方和。由二次曲线外推预测法的模型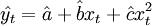 ,有
,有
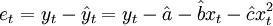
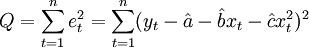 (3.2.2)
(3.2.2)
与拟合直线外推法相同的原理,对式(3.2.2)求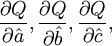 并分别令其等于0,则可得关于
并分别令其等于0,则可得关于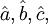 的方程组
的方程组
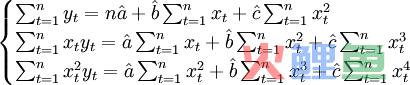 (3.2.3)
(3.2.3)
由于xt表示时间序列的编号,如同拟合直线方程法一样,当时间序列观察期的项数为奇数时,令其中间项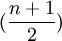 的编号为0,则
的编号为0,则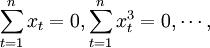
式(3.2.3)可简化为:
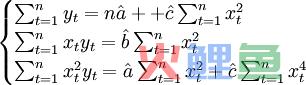 (3.2.4)
(3.2.4)
解上面的方程组可得:
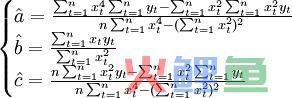 (3.2.5)
(3.2.5)
2) 预测步骤
例3.4某公司1995~2003年的商品销售收入如表3.4所示,试预测该公司2004年的销售收入。
表3.4某公司1995~2003年商品销售收入数据表 (单位:万元) 年份1995199619971998 19992000200120022003 销售收入545641764923 11071322 1568 18362140解:
①绘制散点图如图3.3所示。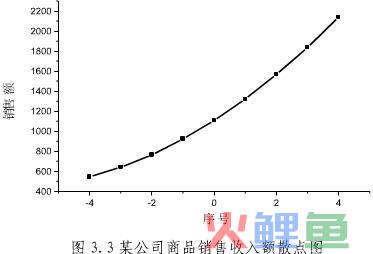
②根据观察值的散点图的变化趋势确定其属于二次曲线变化趋势后,列表计算二次曲线待定参数所需的数据。计算结果如表3.5所示。
③计算待定参数,建立预测模型,并计算预测值。
利用表3.5中的有关数据,代入式(3.2.5)中,计算得:
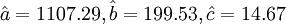
该例的二次曲线的趋势外推预测模型为:
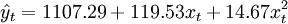 (3.2.6)
(3.2.6)
当x_t=5时,代入上式得
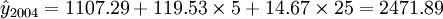 (万元)
(万元)
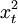
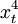 xtyt
xtyt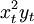
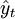
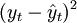 1995-45451625621808720543.891.23
1996-3641981-19235769640.730.07
1997-2764416-15283056766.918.47
1998-192311-923923922.430.32
19990110700001107.290.08
20001132211132213221321.490.26
200121568416313662721565.038.82
2002318369815508165241837.913.65
200342140162568560342402140.130.02
1995-45451625621808720543.891.23
1996-3641981-19235769640.730.07
1997-2764416-15283056766.918.47
1998-192311-923923922.430.32
19990110700001107.290.08
20001132211132213221321.490.26
200121568416313662721565.038.82
2002318369815508165241837.913.65
200342140162568560342402140.130.02
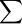 01084660708119727682622.92
01084660708119727682622.92
