排队论的 排队系统模型的基本组成部分

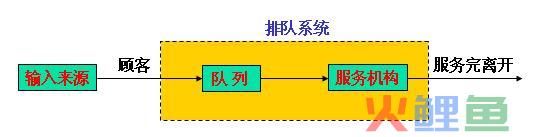
　　排队系统又称服务系统。服务系统由服务机构和服务对象（顾客）构成。服务对象到来的时刻和对他服务的时间（即占用服务系统的时间）都是随机的。图1为一最简单的排队系统模型。排队系统包括三个组成部分：输入过程、排队规则和服务机构。

　　

输入过程

　　输入过程考察的是顾客到达服务系统的规律。它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述，一般分为确定型和随机型两种。例如，在生产线上加工的零件按规定的间隔时间依次到达加工地点，定期运行的班车、班机等都属于确定型输入。随机型的输入是指在时间t内顾客到达数 n（t）服从一定的随机分布。如服从泊松分布,则在时间t内到达n个顾客的概率为

　　

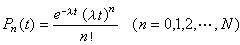
　　或相继到达的顾客的间隔时间T 服从负指数分布，即

　　

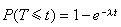
　　式中λ为单位时间顾客期望到达数，称为平均到达率；1/λ为平均间隔时间。在排队论中，讨论的输入过程主要是随机型的。

排队规则

　　排队规则分为等待制、损失制和混合制三种。当顾客到达时，所有服务机构都被占用，则顾客排队等候，即为等待制。在等待制中，为顾客进行服务的次序可以是先到先服务，或后到先服务，或是随机服务和有优先权服务（如医院接待急救病人）。如果顾客来到后看到服务机构没有空闲立即离去，则为损失制。有些系统因留给顾客排队等待的空间有限，因此超过所能容纳人数的顾客必须离开系统，这种排队规则就是混合制。

服务机构

　　可以是一个或多个服务台。多个服务台可以是平行排列的，也可以是串连排列的。服务时间一般也分成确定型和随机型两种。例如，自动冲洗汽车的装置对每辆汽车冲洗（服务）时间是相同的，因而是确定型的。而随机型服务时间v 则服从一定的随机分布。如果服从负指数分布，则其分布函数是

　　

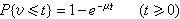
　　式中μ为平均服务率，1/μ为平均服务时间。