排队论的 排队系统的分类
-
-
凡老师 这家伙很懒，还没有设置简介...
0 人点赞了该文章 · 13 浏览
如果按照排队系统三个组成部分的特征的各种可能情形来分类，则排队系统可分成无穷多种类型。因此只能按主要特征进行分类。一般是以相继顾客到达系统的间隔时间分布、服务时间的分布和服务台数目为分类标志。现代常用的分类方法是英国数学家D.G.肯德尔提出的分类方法，即用肯德尔记号 X/Y/Z进行分类。
X处填写相继到达间隔时间的分布；
Y处填写服务时间分布;
Z处填写并列的服务台数目。
各种分布符号有：M-负指数分布;D-确定型; Ek-k阶埃尔朗分布；GI-一般相互独立分布；G-一般随机分布等。这里k阶埃尔朗分布是指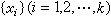为相互独立且服从相同指数分布的随机变量时，
服从自由度为 2k的χ2分布。例如,M/M/1表示顾客相继到达的间隔时间为负指数分布、服务时间为负指数分布和单个服务台的模型。D/M/C表示顾客按确定的间隔时间到达、服务时间为负指数分布和C个服务台的模型。至于其他一些特征,如顾客为无限源或有限源等，可在基本分类的基础上另加说明。
